数据结构-单向链表
1. 内容大纲
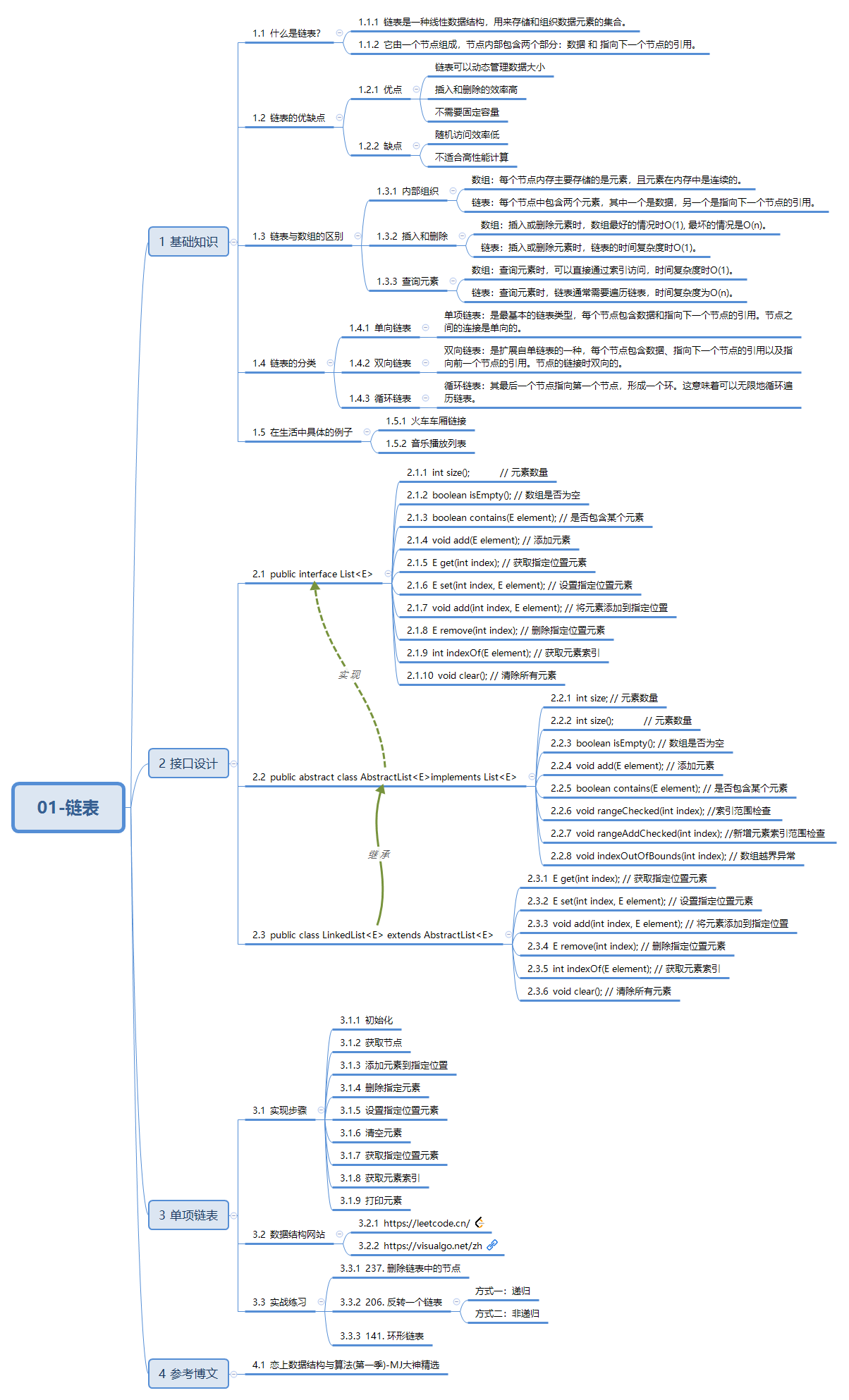
2. 基础知识
2.1. 什么是链表
链表是一种线性的数据结构,主要存储和组织元素的一个集合节点。
2.2. 链表优缺点
优点
- 链表可以动态管理数据大小:链表可以根据节点动态分配内存,不需要分配固定大小的内存。
- 插入和删除的效率高:由于我们插入和删除时,只需要更改节点的指针,而不需要大量移动元素。
- 不需要固定容量。
缺点
- 随机访问效率低:当我们查找一个元素时,需要从头找到尾因此最好情况时间复杂度是O(1),最坏时间复杂度是O(n)。
- 不适合高性能计算。
2.3. 链表的分类
链表的分类存在很多种,但如我们目前只讨论如下三种情况:
单向链表:单向链表是最基本的链表类型,每个节点包含数据和指向下一个节点的引用,节点之间的连接是单向的。
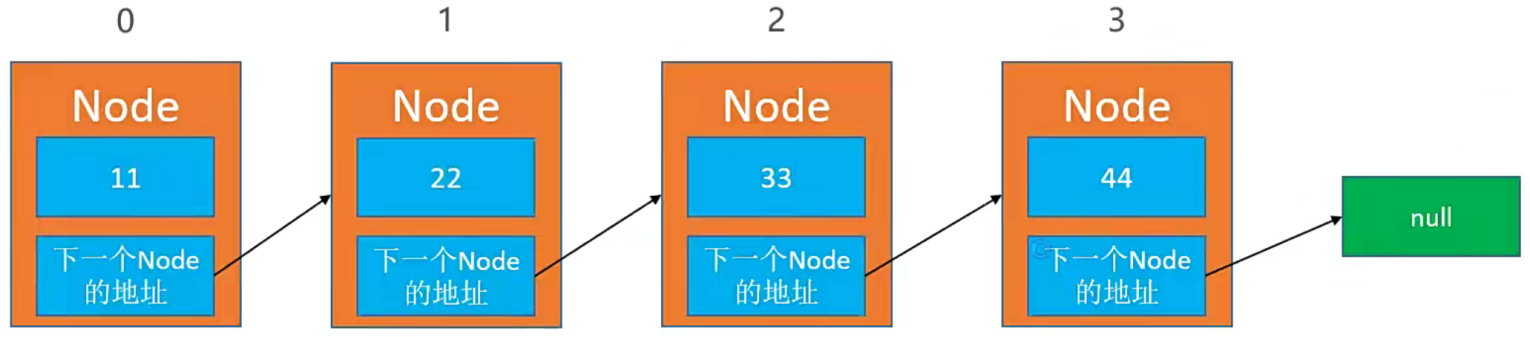
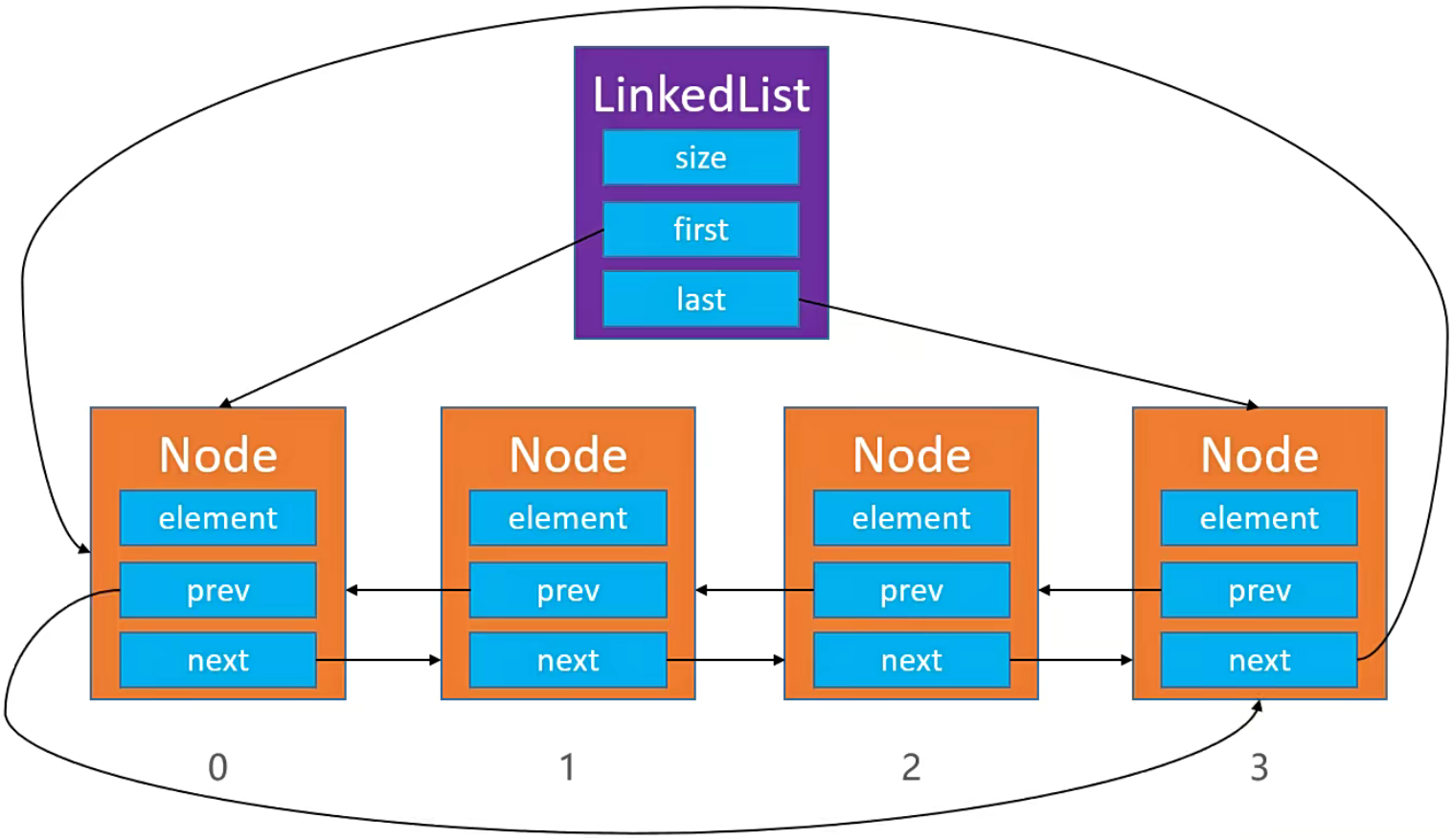
双向链表:双向链表是扩展自单链表的一种,每个节点包含数据、指向下一个节点的引用以及指向前一个节点的引用。节点的连接是双向的。
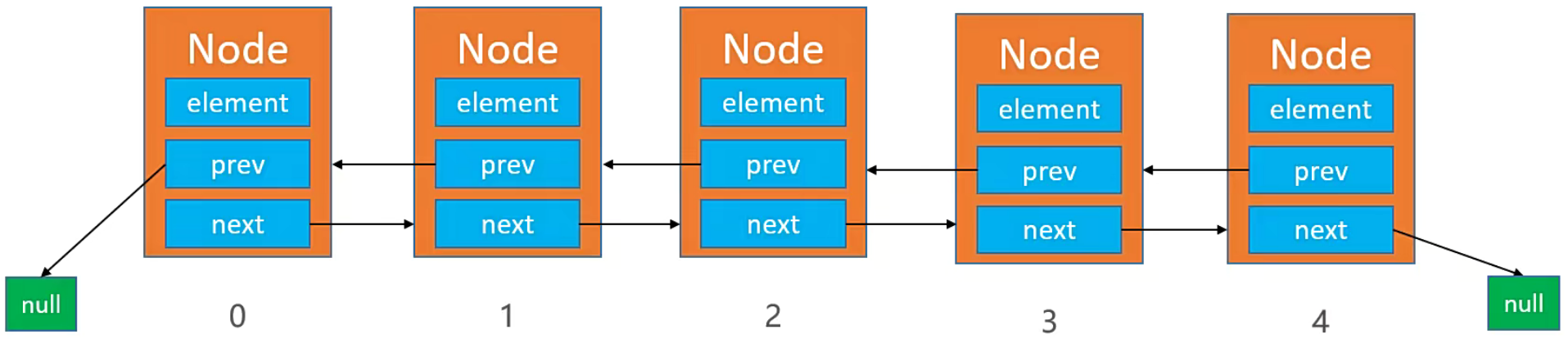
循环链表:循环链表是一种链表,其最后一个节点指向第一个节点,形成一个环。这意味着可以无限地循环遍历链表。
3.1. 单向循环链表:
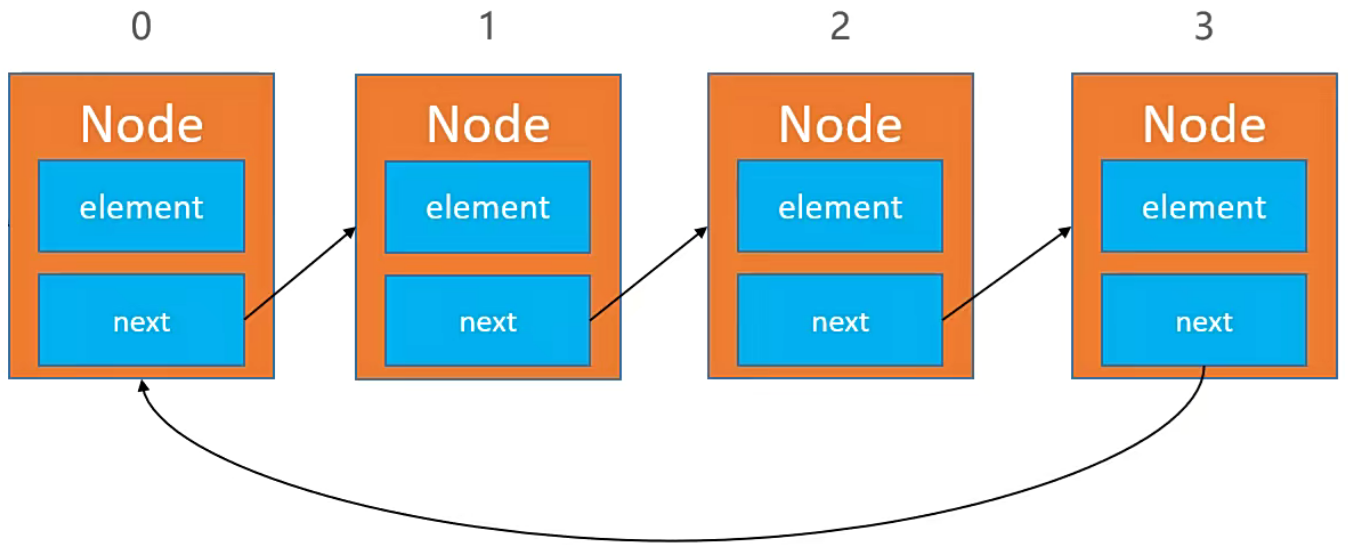
3.2. 双向循环链表:
2.4. 生活中具体的例子
- 火车车厢链接:火车的车厢满足链表这种数据结构。火车有具体的编号,乘客类似于数据,车厢必须要与下一节车厢连接。
- 音乐播放列表:音乐播放列表足链表这种数据结构。当前播放的音乐必须知道下一首和上一首歌曲是什么。
3. 接口设计
我们从动态数组中我们可以再次对
List集合进行优化,我们将公共部分进行封装为AbstractList。
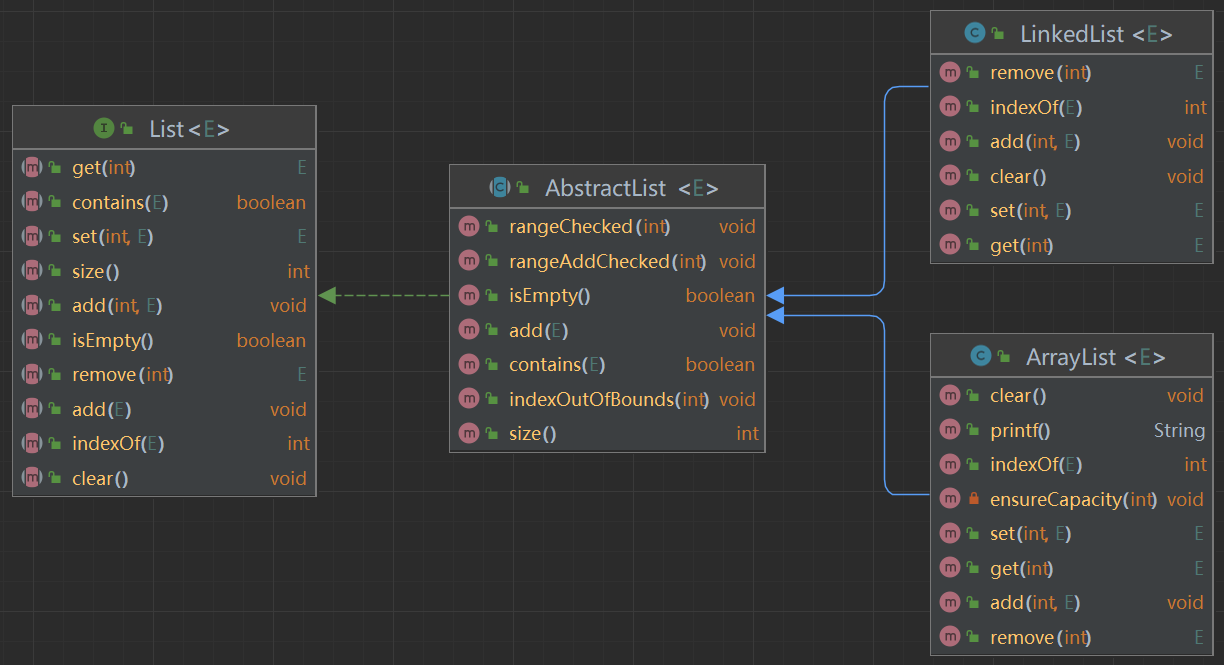
List<E>.java
1 | public interface List<E> { |
AbstractList<E>.java
1 | public abstract class AbstractList<E> implements List<E> { |
LinkedList<E>.java
1 | public class LinkedList<E> extends AbstractList<E>{ |
4. 代码实现
4.1. 初始化
需求:我们初始化一个原始的链表节点元素。
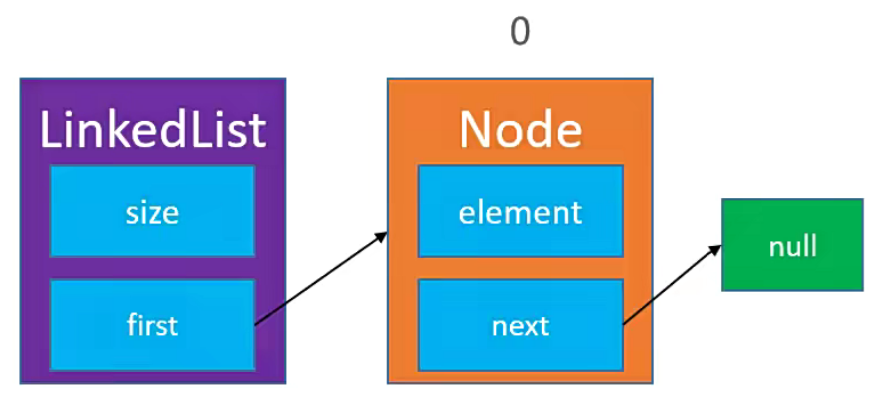
实现步骤
- 初始化类
LinkedList<E>,其中存放两个元素,第一个元素存放size, 第二个元素指向下一个节点。 - 创建节点
Node<E>,其中也是存放两个元素,第一个元元素存放element,第二个元素存放下一个节点的引用。
1 | public class LinkedList<E> extends AbstractList<E>{ |
4.2. 获取节点
需求:通过
index索引获取Node节点。

实现步骤
- 例如,我们需要获取索引为 2 的节点,那就是通过
first.next.next直接就获取到了索引为 2 的Node节点。 - 首先,我们找到头节点。
- 然后,我们在通过索引的遍历直接找到对应的
Node节点即可。
具体代码
1 | /** |
4.3. 添加元素到指定位置
需求:我们需要将新的节点添加到节点为 0 的后面
注意:我们需要考虑添加到 0 节点的位置和最后一个节点的位置
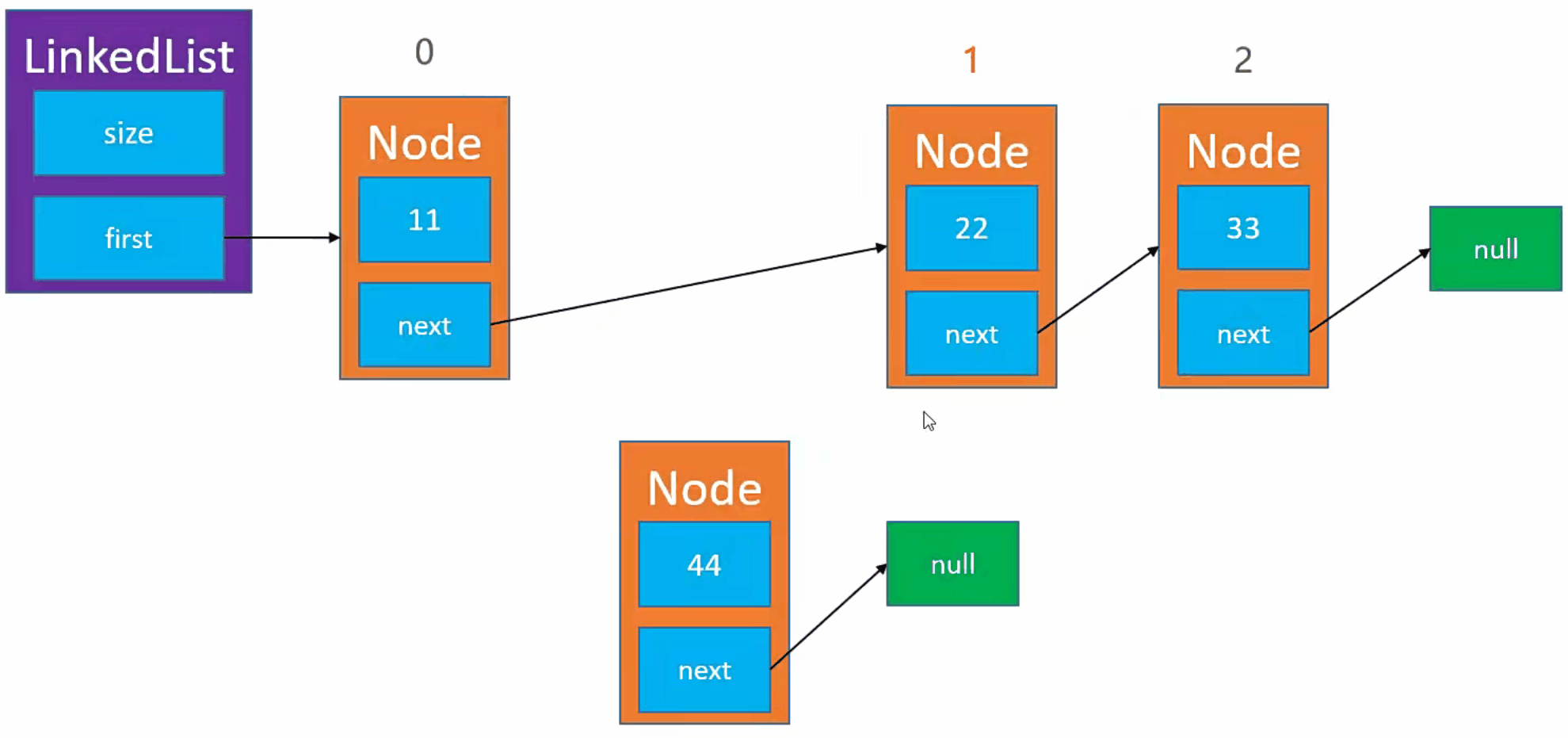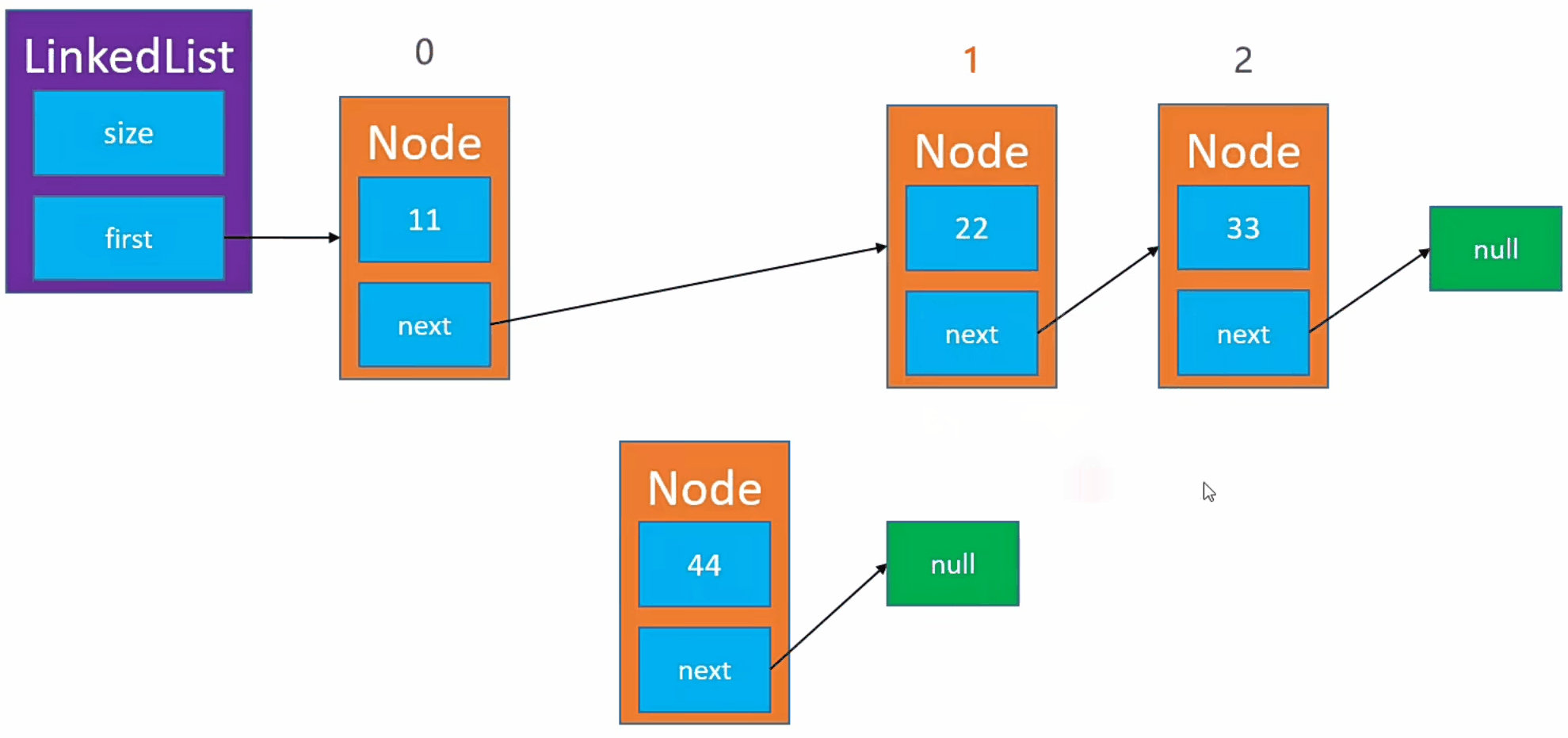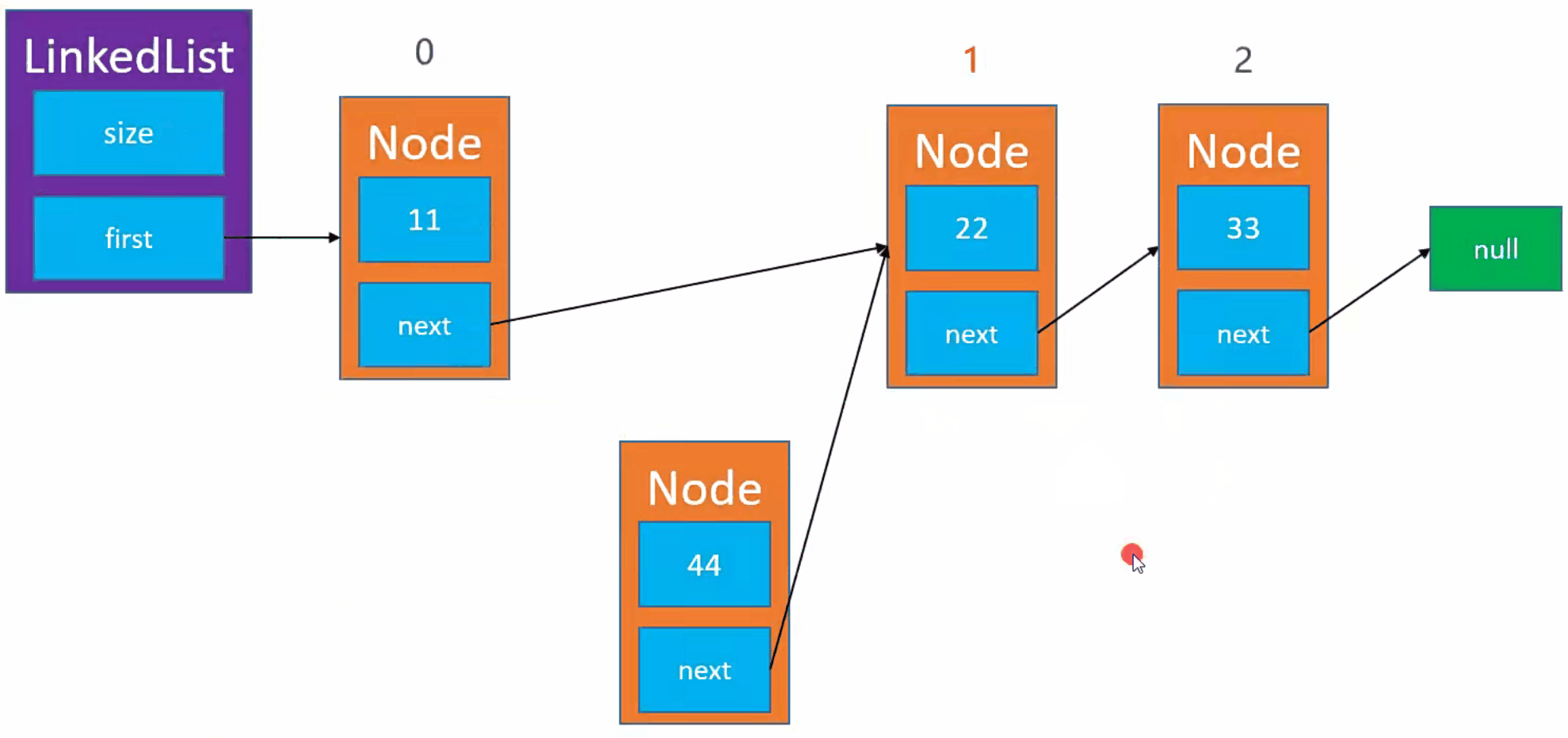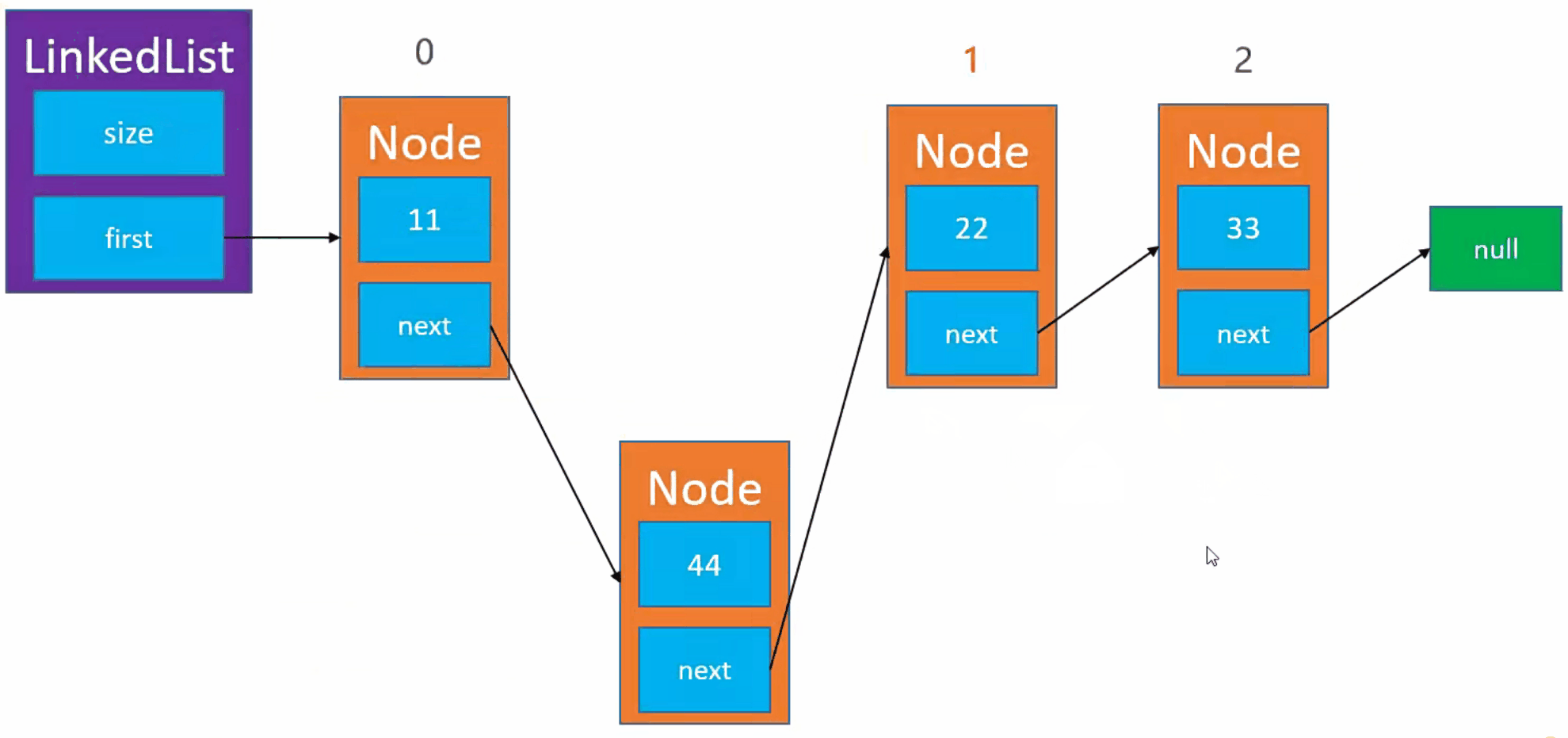
实现步骤
- 例如,我们需要将新节点(
Node)元素添加到index为 1 的位置。 - 首先,我们需要找到
index为 1 的节点。 - 然后,我们需要将新节点(
Node)的next指向index = 1的节点。 - 最后,我们将上一个节点的
next指向 新节点(Node)。 - 注意,我们需要考虑
index = 0的情况。
具体代码
1 | /** |
4.4. 设置指定位置元素
需求:设置指定位置元素
1 | /** |
4.5. 删除指定元素
需求:我们删除
index=1这个元素。
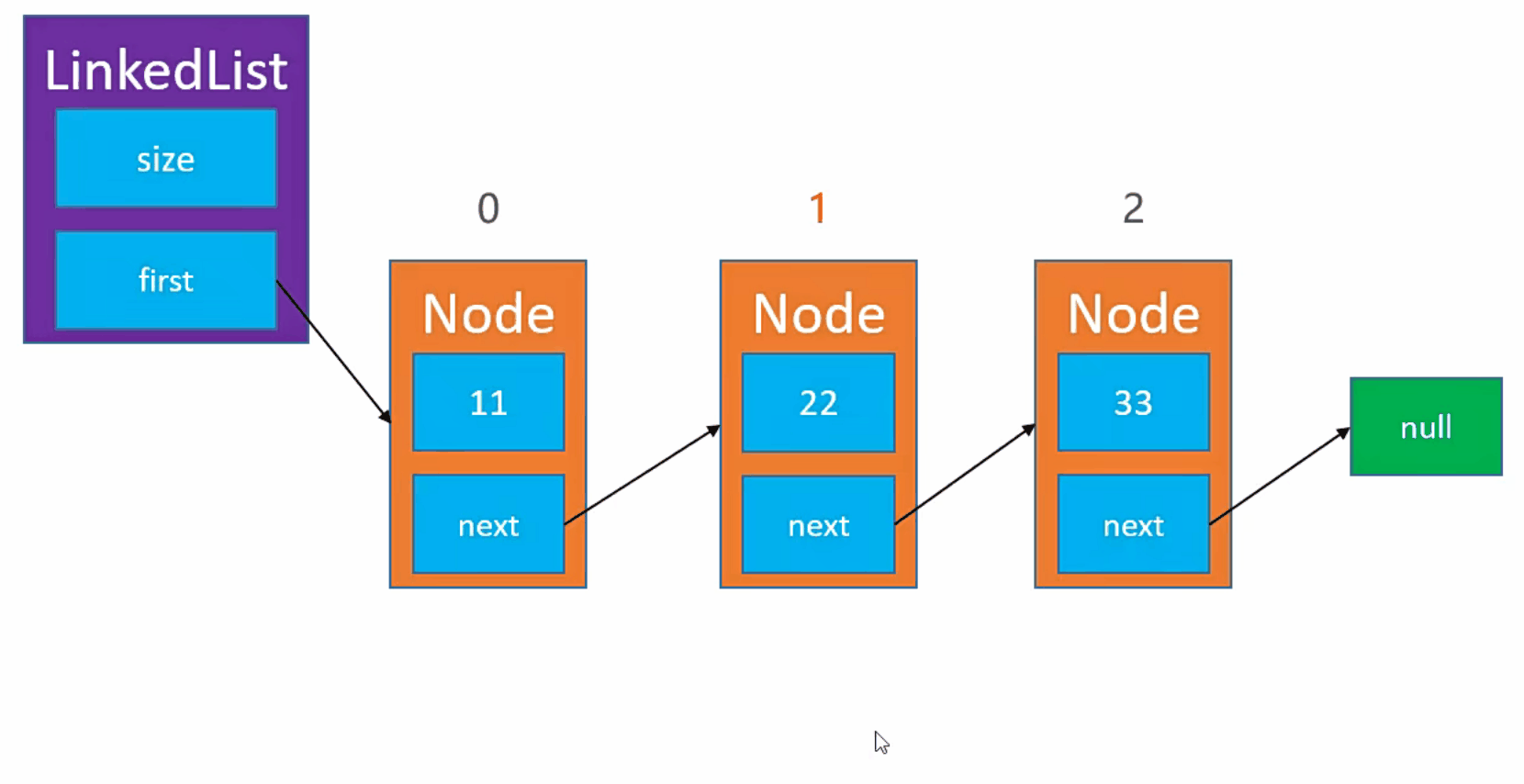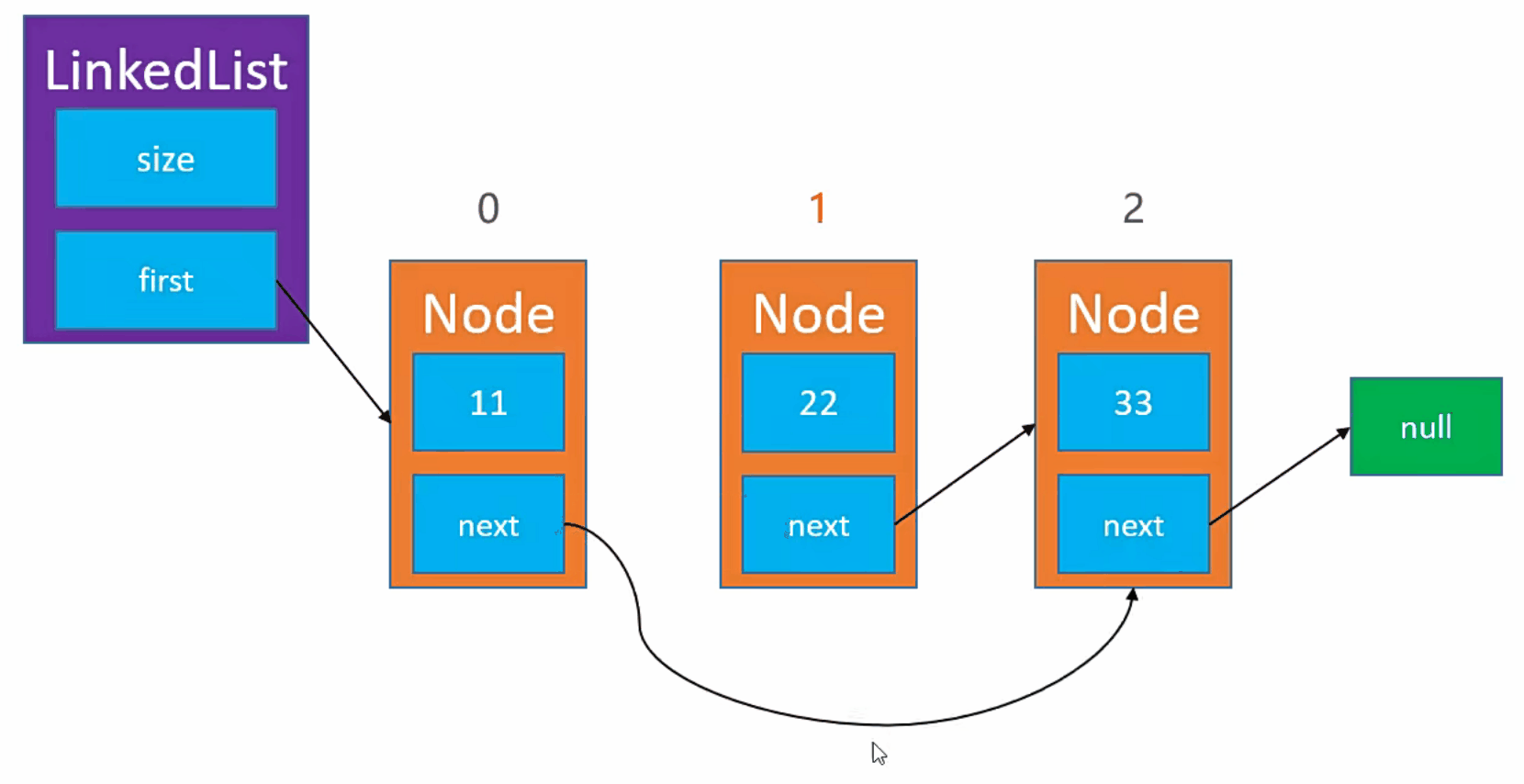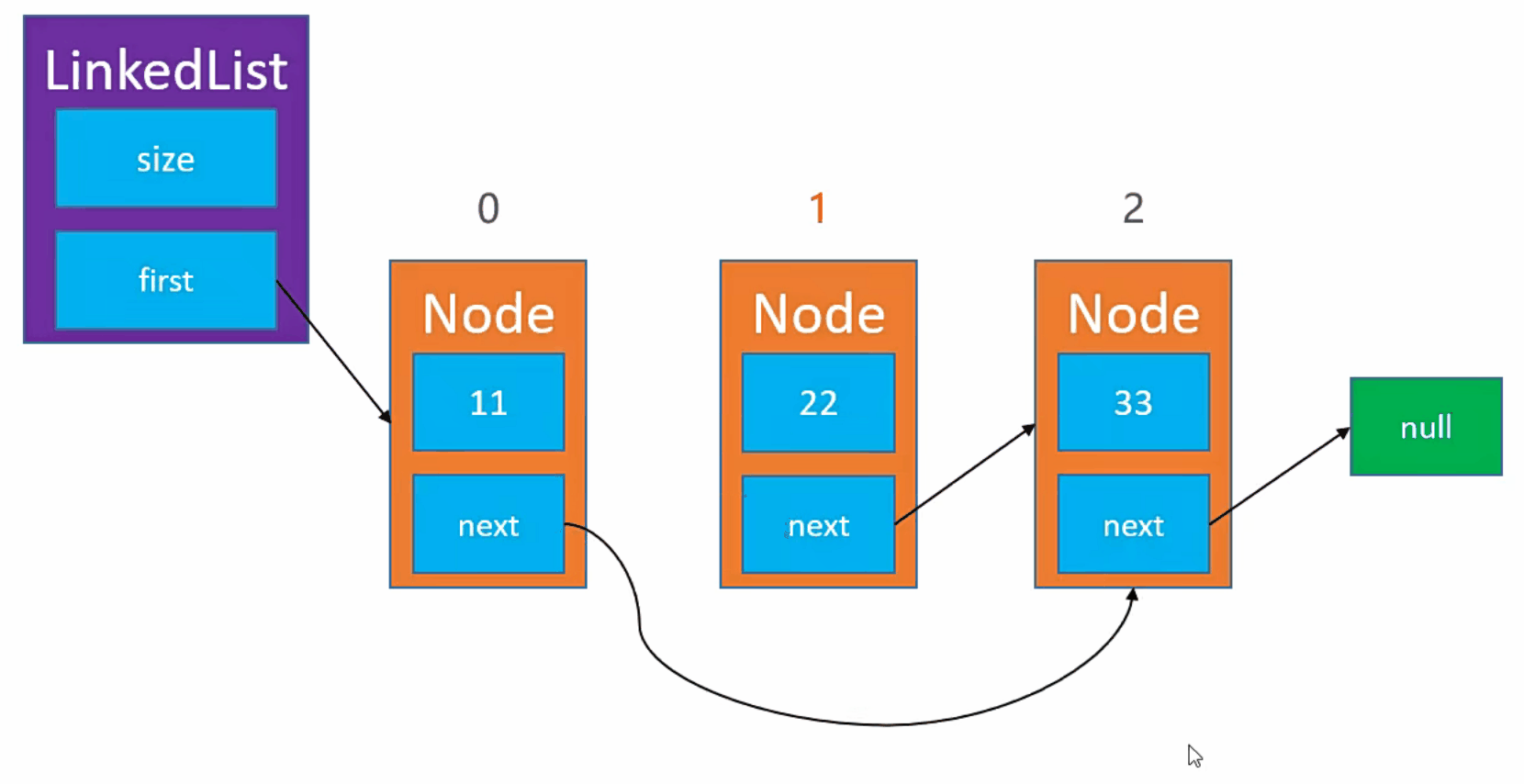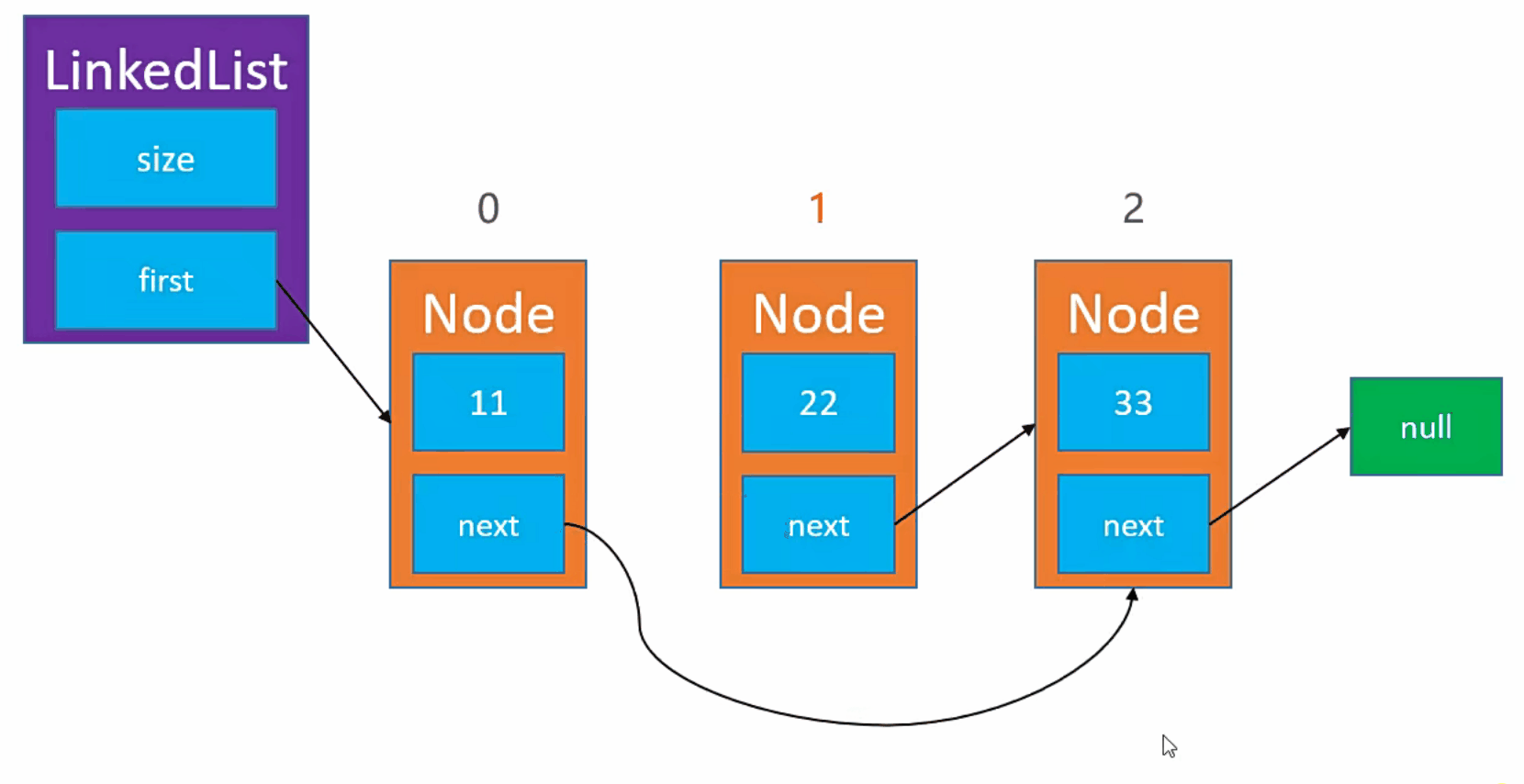
实现步骤
- 例如,我们需要删除
index为 1 的节点。 - 首先,我们获取当前节点信息。【node(index)】
- 然后,我们获取到当前节点的下一个节点信息。【node(index).next】
最后,我们获取当前节点的上一个节点信息,指向当前节点的下一个节点。【node(index - 1).next = node(index).next】
注意,我们需要考虑
index = 0的情况。
具体代码
1 | /** |
4.6. 清空元素
需求:清空所有元素。
1 | /** |
4.7. 获取指定位置元素
需求:获取指定位置元素。
1 | /** |
4.8. 获取元素索引
需求:根据给定的元素,找到对应的索引
1 | /** |
4.9. 打印元素
需求:打印节点元素
1 | /** |
4.10. 测试用例
1 | public class LinkedListTest { |
5. 实战练习
如下练习题主要来源于 LeetCode
5.1. 删除链表中的节点
地址:https://leetcode.cn/problems/delete-node-in-a-linked-list/description/
需求如下:
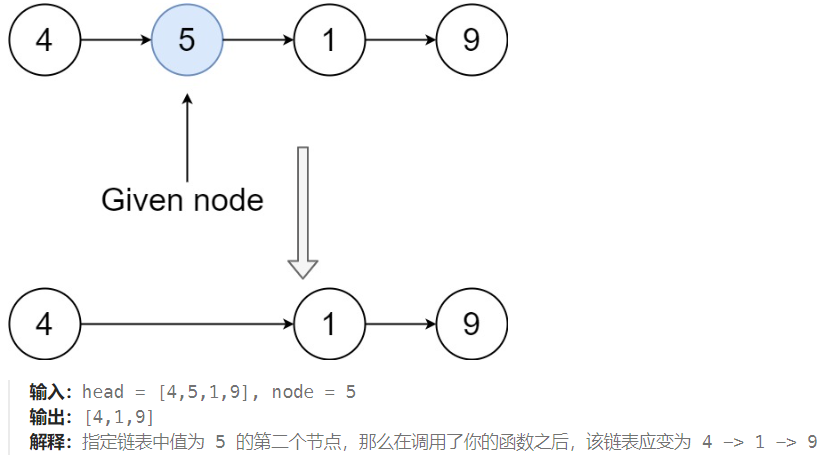
- 实现方案:
- 方案一:如果能获取到当前节点【5】的上一个节点【4】,然后再通过节点【4】指向下下个节点【1】,就解决问题了,但我们无法获取到节点【4】。
- 方案二(实践方案):如果我们不走节点,而是移动节点内的元素,这个问题就很好解决了。
- 实现步骤:
- Step-1:我们将当前节点【5】(的下一个节点【1】元素覆盖掉当前节点【5】元素。==》
node.element = node.next.element; - Step-2:我们在将当前节点【1】指向到下下个节点【9】。 ==》
node.next= node.next.next;
- Step-1:我们将当前节点【5】(的下一个节点【1】元素覆盖掉当前节点【5】元素。==》
- 实现代码:
1 | public class ListNode { |
5.2. 反转一个链表
地址:https://leetcode.cn/problems/reverse-linked-list/description/
需求如下:

实现方式:
- 方式一(递归法):递归就是自己调用自己,其核心思想是反转剩余部分的链表,然后再处理当前节点。
- 方式二(迭代法):通过改变当前节点的下一指针指向,实现局部反转,再通过移动节点顺序扩展到全局反转。
5.2.1. 递归法
实现步骤:
- 思路:递归分为两个部分,第一个部分是寻找出口,第二个部分是处理拆分后每个节点的逻辑。
- Step-1:首先,我们的出口应该满足当前节点为空,或者当前节点的 next 为空。
head == null || head.next == null。 - Step-2:然后,我们在处理逻辑部分,首先我们需要知道那个节点先出来。
head -> ListNode{val=4, next=ListNode{val=5, next=null}}。 - Step-3:最后,处理共同的逻辑。
head.next.next = head、head.next = null。
- 代码实现:
1 | public class _206_反转链表 { |
5.2.2. 迭代法
实现步骤:
进入的数据:
ListNode{val=1, next=ListNode{val=2, next=null}}定义一个临时节点
tempNode初始化为null- 当头节点head不为空时,进入循环
- 保存head的下一个节点为
nextNode - 将head的next指针指向
tempNode实现局部反转 - 将head赋值给
tempNode保存反转后的部分链表 - head移动到
nextNode继续下一次反转 - 循环结束后
tempNode指向反转后的链表 - 返回
tempNode作为新链表的头节点
1 | public static ListNode reverseList2(ListNode head) { |
5.3. 环形链表
- 需求如下:
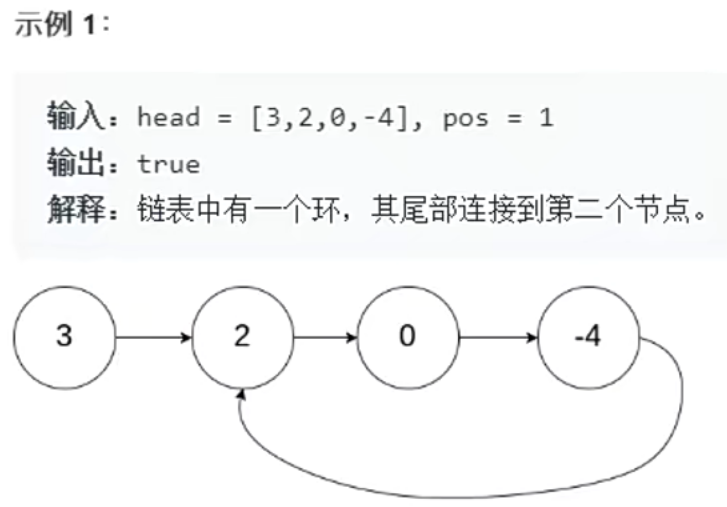
实现方式
- 快慢指针:通过快慢指针进行解决问题,例如在一个操场跑步,一个快一个慢,他们总会相遇。
实现步骤
- 主要使用快慢指针进行实现,慢指针走一步,快指针走两步,如果存在环那么他们一定会相遇。
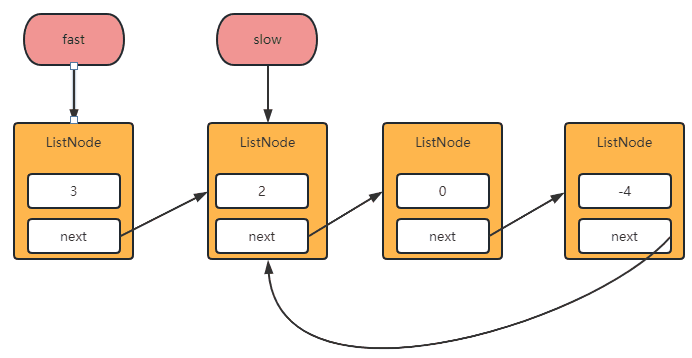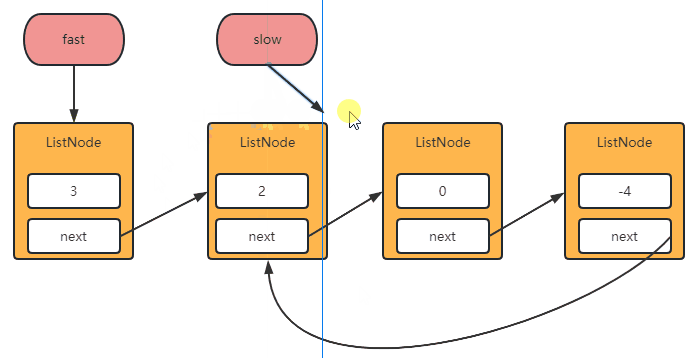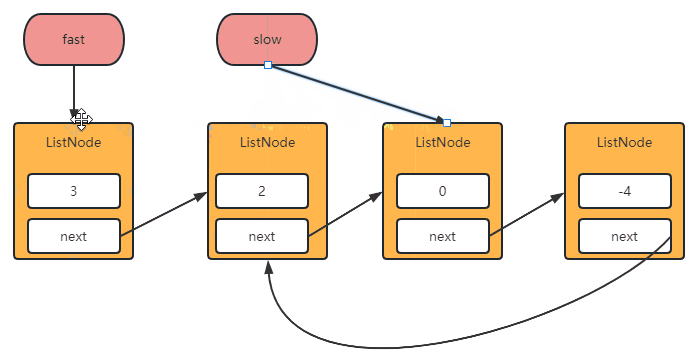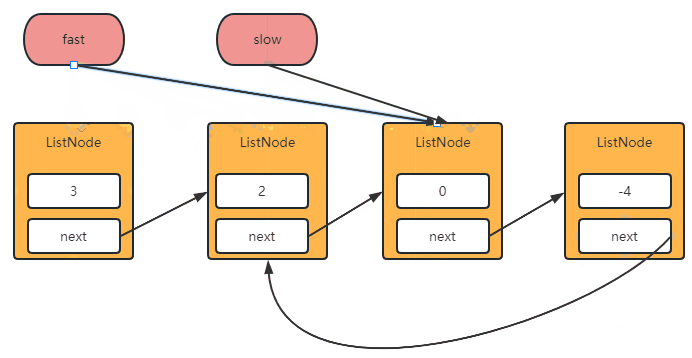
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) return false;
ListNode slow = head;
ListNode fast = head.next;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) return true;
}
return false;
}






