1. 内容大纲
本章节代码:https://github.com/wicksonZhang/data-structure/tree/main/12-BinaryHeap
2. 基础知识
2.1. 二叉堆解决了什么问题
二叉堆解决的主要问题是在一个动态集合中找到最大或最小元素,并且支持快速的插入和删除操作。
- 找到最大或最小元素的时间复杂度:O(1)
- 删除和插入的时间复杂度:O(logn)
2.2. 二叉堆是什么
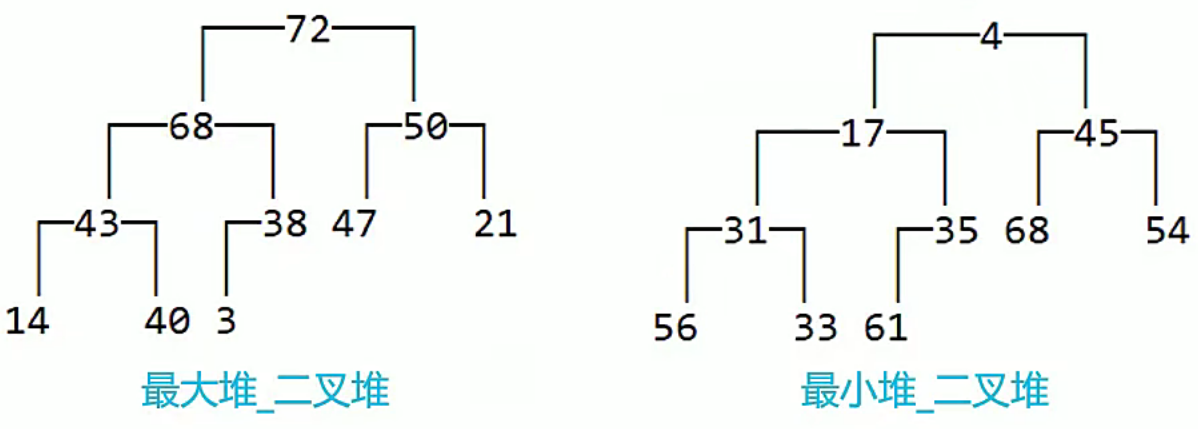
二叉堆(Binary Heap):二叉堆是一种特殊的二叉树数据结构,二叉堆的核心概念如下:
- 堆(heap):任意节点 i 的值总是 大于等于(>=) 或者 小于等于(<=) 子节点 的值。
- 最大堆(Max Heap): 对于任意节点 i 的值如果 大于等于(>=) 子节点 的值。
- 最小堆(Min Heap):对于任意节点 i 的值如果 小于等于(<=)子节点 的值。
2.3. 二叉堆的性质
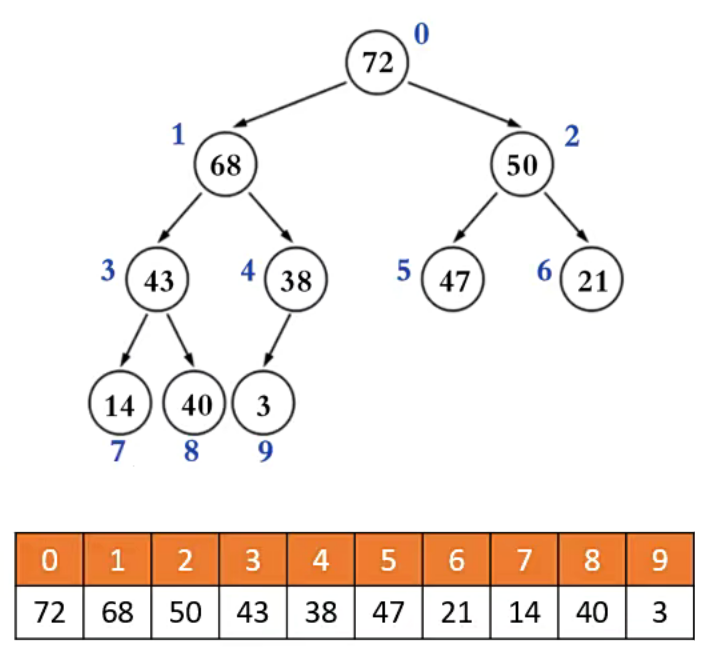
二叉堆的本质上是一颗完全二叉树,所以二叉堆的索引 i 具备以下性质:
- 注意,以下的 i 代表的是索引,n 代表的是元素数量。
- 如果 i = 0,它是根节点。
如果 i > 0,它的父节点的索引为 floor((i - 1) / 2)。
- 例如,节点 43、38 的父节点都是 68。 floor((3 - 1) / 2) = 1
如果 2i + 1 <= n - 1,它的左子节点的索引为 2i + 1。
- 例如,节点 68 的左子节点 43。2 * 1 + 1 = 3
如果 2i + 1 > n - 1,它无左子节点。
- 例如,节点 47 无左子节点。2 * 5 + 1 > 10 -1
如果 2i + 2 <= n - 1,它的右子节点的索引为 2i + 2。
- 例如,节点 68 的右子节点就是 38。2 * 1 + 2 = 4
如果 2i + 2 > n - 1,它无右子节点。
- 例如,节点47。2 * 5 + 2 > 10 - 1
2.4. 二叉堆优缺点
优点
- 高效的插入和删除操作: 二叉堆对于插入和删除操作的时间复杂度都是 O(log n),其中 n 是堆中元素的数量。
- 高效的查找最大值或最小值:如果是最大堆或者是最小堆,根节点就是最大值或者最小值,时间复杂度为O(1)。
缺点
- 不支持动态大小:因为二叉堆一般底层可以采用数组实现,所以是不具备动态扩容的。
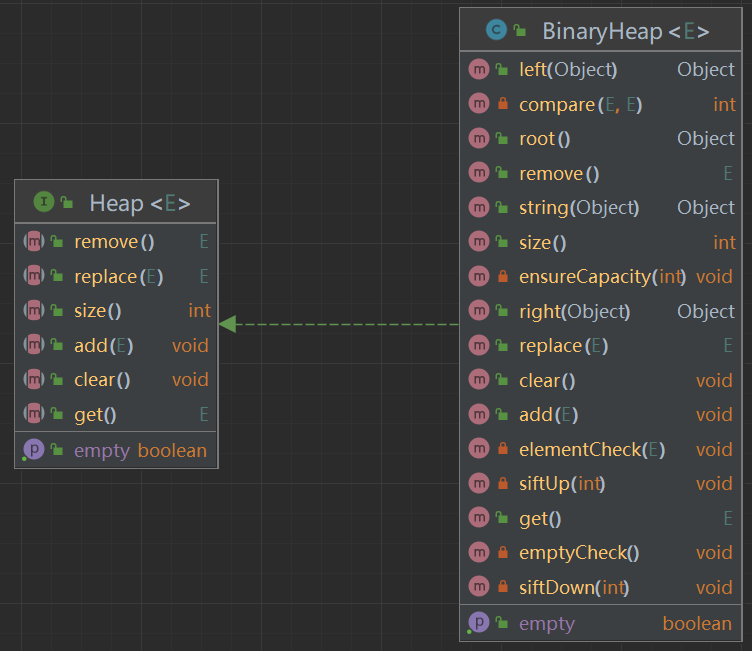
3. 接口设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
public interface Heap<E> {
int size();
boolean isEmpty();
void clear();
void add(E e);
E get();
E remove();
E replace(E e);
}
|
4. 代码实现
4.1. 初始化元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
@SuppressWarnings("unchecked")
public class BinaryHeap<E> implements Heap<E> {
private E[] elements;
private int size;
private static final int DEFAULT_CAPACITY = 1 << 4;
private Comparator<E> comparator;
public BinaryHeap() {
this(null);
}
public BinaryHeap(Comparator<E> comparator) {
this.comparator = comparator;
this.elements = (E[]) new Object[DEFAULT_CAPACITY];
}
private int compare(E element1, E element2) {
if (comparator != null) {
return comparator.compare(element1, element2);
}
return ((Comparable<E>) element1).compareTo(element2);
}
}
|
4.2. 获取堆顶元素
1
2
3
4
5
6
7
8
9
10
11
| @Override
public E get() {
emptyCheck();
return elements[0];
}
private void emptyCheck() {
if (size == 0) {
throw new IndexOutOfBoundsException("Heap is empty");
}
}
|
4.3. 添加元素
实现思路
1
2
3
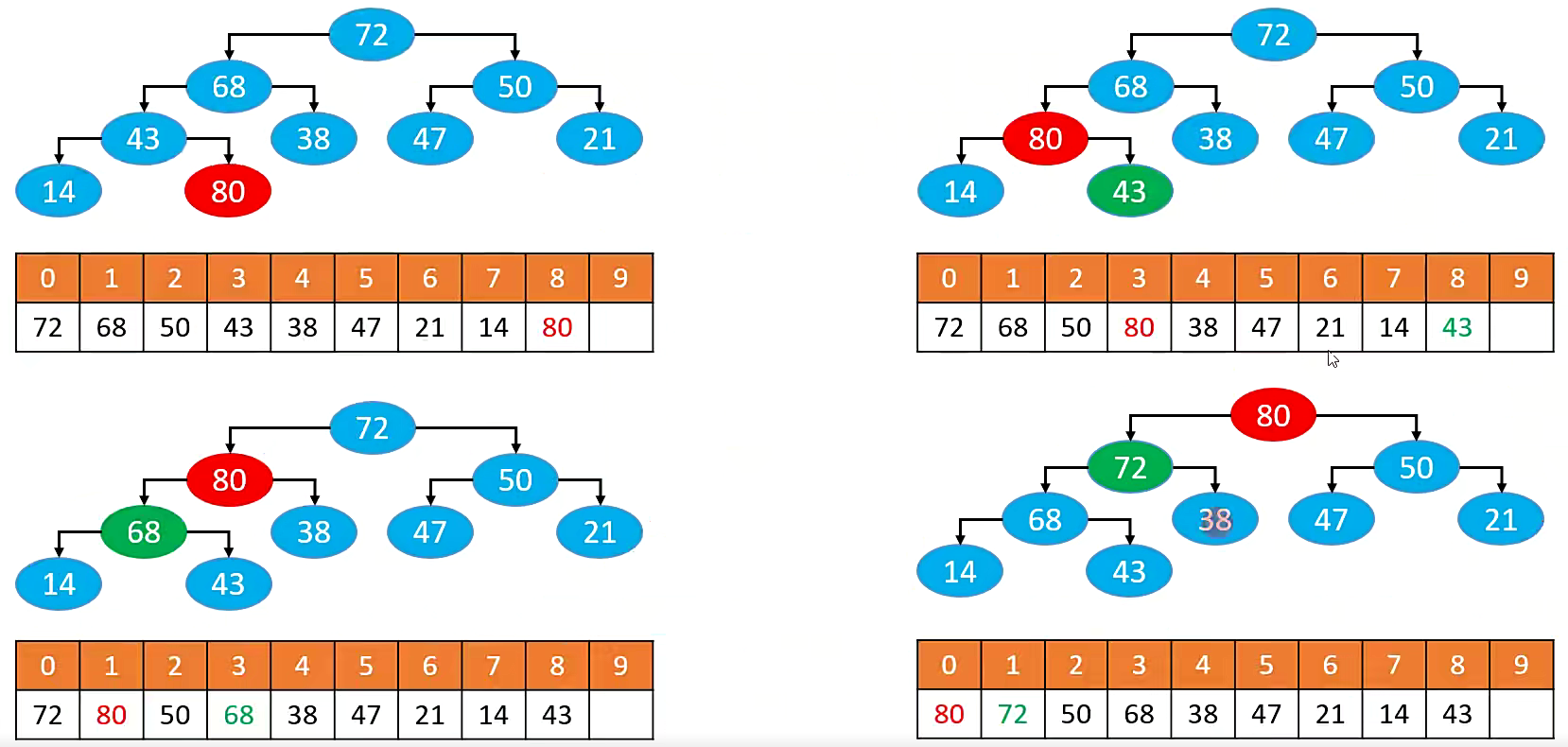
| 1. Step-1: 我们需要将元素添加在数组的最后一个元素。
2. Step-2: 我们通过判断添加的元素是否比父节点大,如果比父节点大就交换位置。
3. Step-3: 一致持续这个操作,最后如果没有父级节点就推出循环。
|
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
@Override
public void add(E element) {
elementCheck(element);
ensureCapacity(size + 1);
elements[size++] = element;
siftUp(size - 1);
}
private void ensureCapacity(int capacity) {
if (capacity - elements.length > 0) {
int newCapacity = capacity + (capacity >> 1);
E[] newElement = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newElement[i] = elements[i];
}
elements = newElement;
}
}
private void siftUp(int index) {
E element = elements[index];
while (index > 0) {
int parentIndex = index - 1 >> 2;
E parentElement = elements[parentIndex];
if (compare(parentElement, element) >= 0) {
break;
}
elements[index] = parentElement;
index = parentIndex;
}
elements[index] = element;
}
private void elementCheck(E e) {
if (e == null) {
throw new NullPointerException("Element is not null");
}
}
|
4.4. 删除
实现思路
- 这个不能使用常规思维进行解决,如果直接删除堆顶元素。那么所有的元素需要向前移动,时间复杂度又变为了 O(n) 。
1
2
3
4
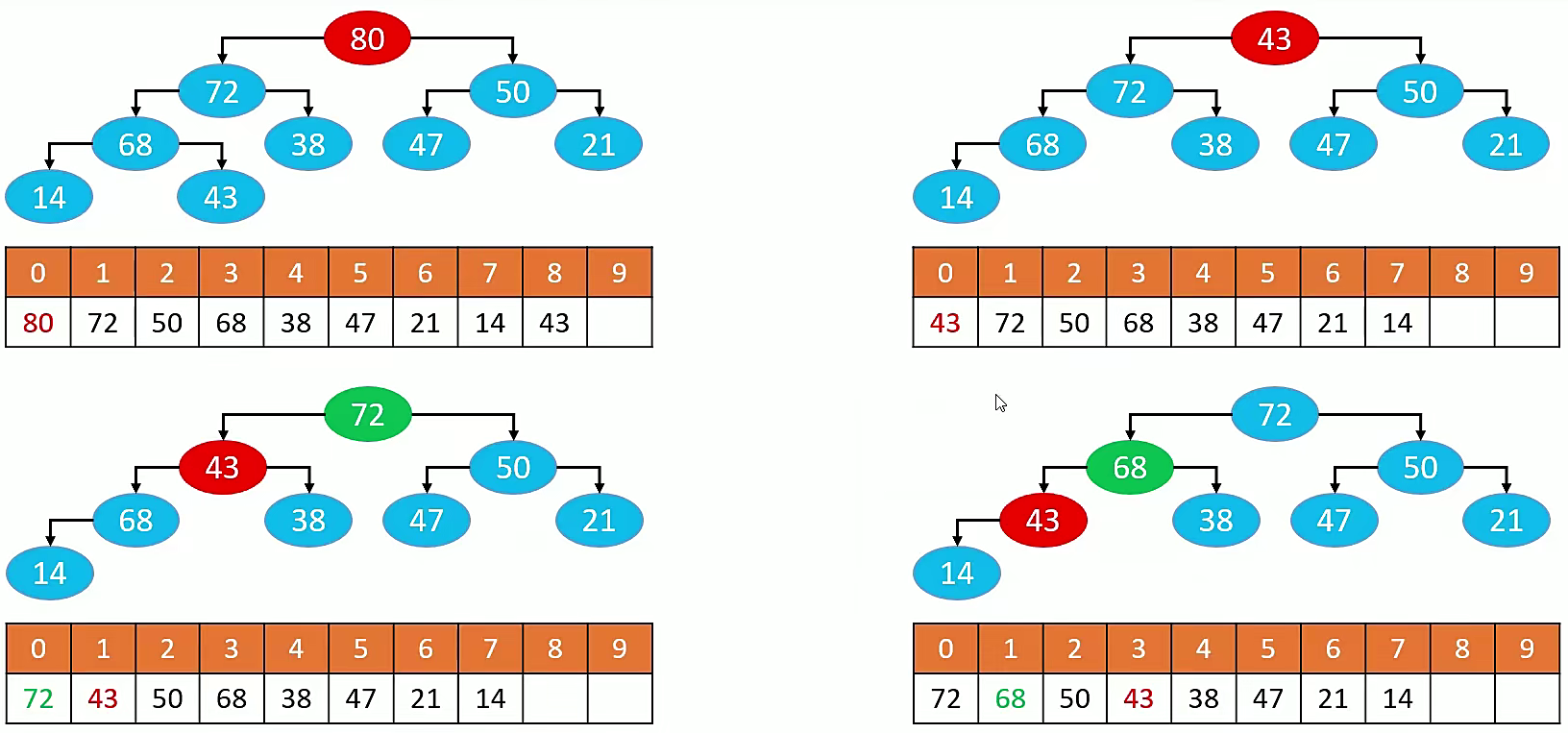
| 1. Step-1: 将堆顶元素与数组最后一个元素进行交换位置,然后将最后一个元素删除。
2. Step-2: 再将新的堆顶元素与子节点进行比较。
3. Step-3: 如果比子节点小,则将最大子节点的元素进行交换。
4. Step-4: 如果比子节点大,或者没有子节点,则退出循环。
|
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
@Override
public E remove() {
emptyCheck();
int lastIndex = --size;
E root = elements[0];
elements[0] = elements[lastIndex];
elements[lastIndex] = null;
siftDown(0);
return root;
}
private void siftDown(int index) {
E element = elements[index];
int half = size >> 1;
while (index < half) {
int childIndex = (index << 1) + 1;
E child = elements[childIndex];
int rightIndex = childIndex + 1;
if (rightIndex < size && compare(elements[rightIndex], child) > 0) {
child = elements[childIndex = rightIndex];
}
if (compare(element, child) >= 0) break;
elements[index] = child;
index = childIndex;
}
elements[index] = element;
}
|
4.5. 删除堆顶元素同时插入一个新的元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
@Override
public E replace(E element) {
elementCheck(element);
E root = null;
if (size == 0) {
elements[0] = element;
size++;
} else {
root = elements[0];
elements[0] = element;
siftDown(0);
}
return root;
}
|
5. 参考博文












