1. 内容大纲
本章节的代码:https://github.com/wicksonZhang/data-structure/tree/main/2-LinkedList/src/main/java/com/wickson/linkedlist/doubles
2. 基础知识
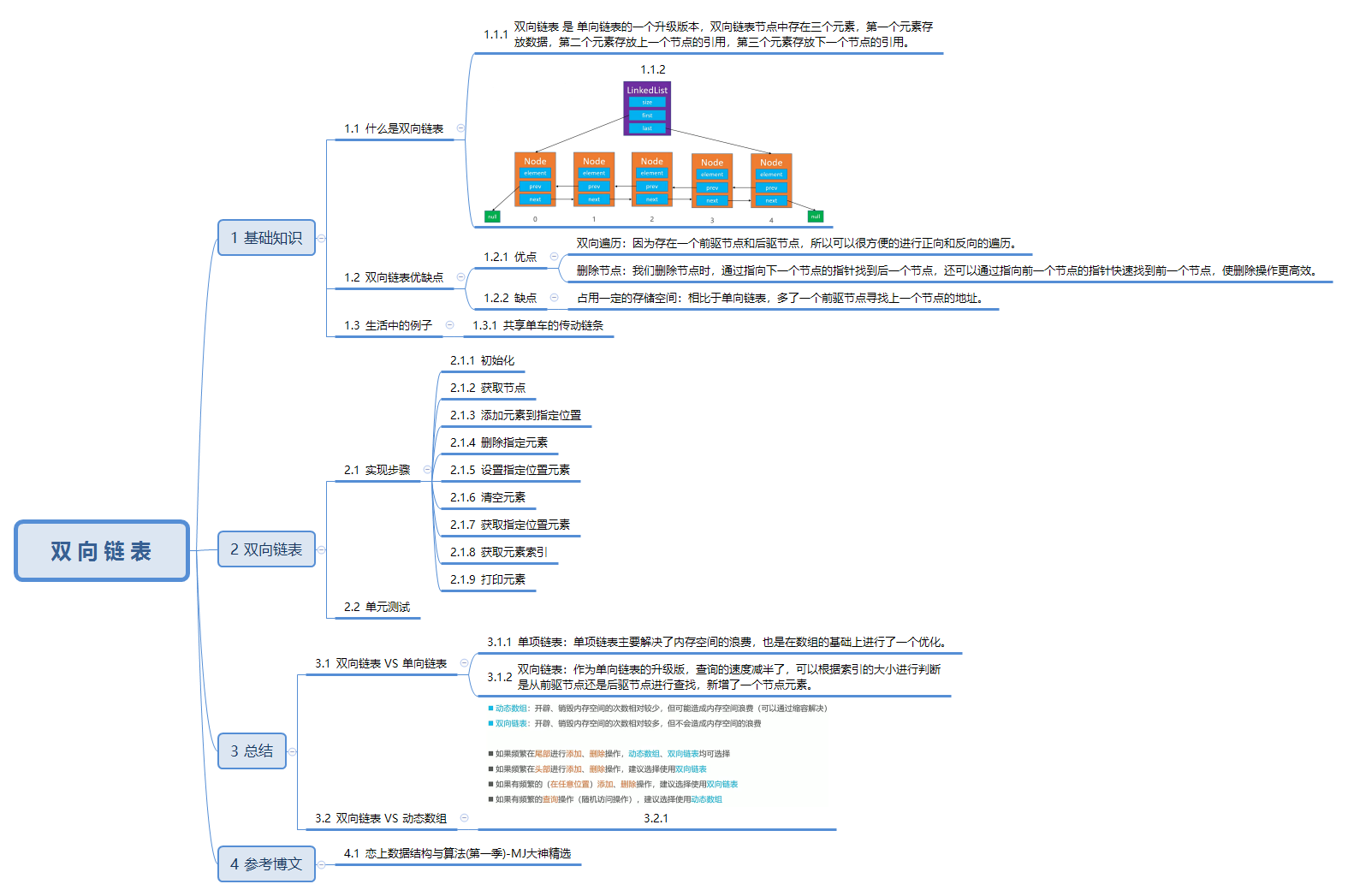
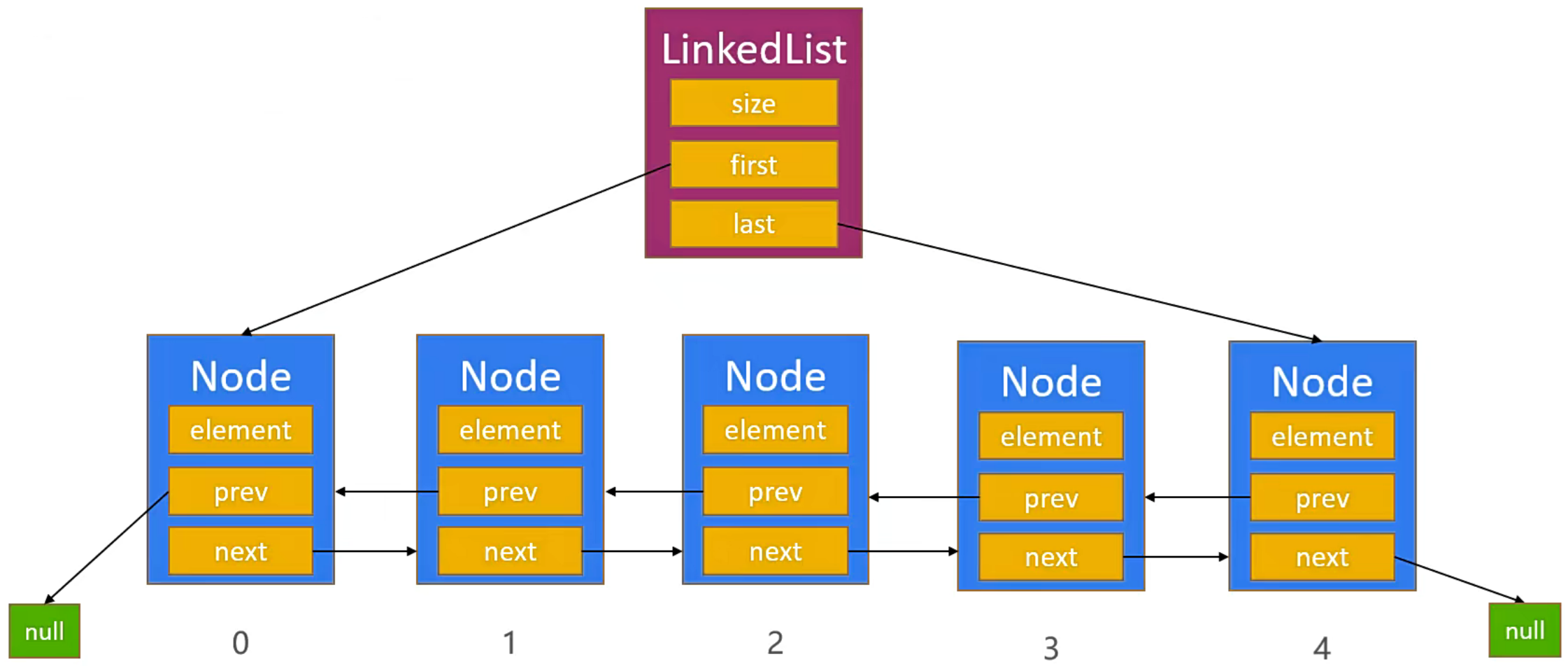
2.1. 什么是双向链表
双向链表是单项链表的一个升级版本,由节点中的两个元素升级为了三个元素。第一个元素指向上一个节点的引用,第二个元素存放数据,第三个元素指向下一个节点的引用。
2.2. 双向链表优缺点
优点
- 双向遍历:因为存在一个前驱节点和后驱节点,所以可以很方便的进行正向和反向的遍历。
- 删除节点:我们删除节点时,通过指向下一个节点的指针找到后一个节点,还可以通过指向前一个节点的指针快速找到前一个节点,使删除操作更高效。
缺点
- 占用一定的存储空间:相比于单向链表,多了一个前驱节点寻找上一个节点的地址。
2.3. 生活中的例子
- 共享单车的传动链条
3. 接口设计
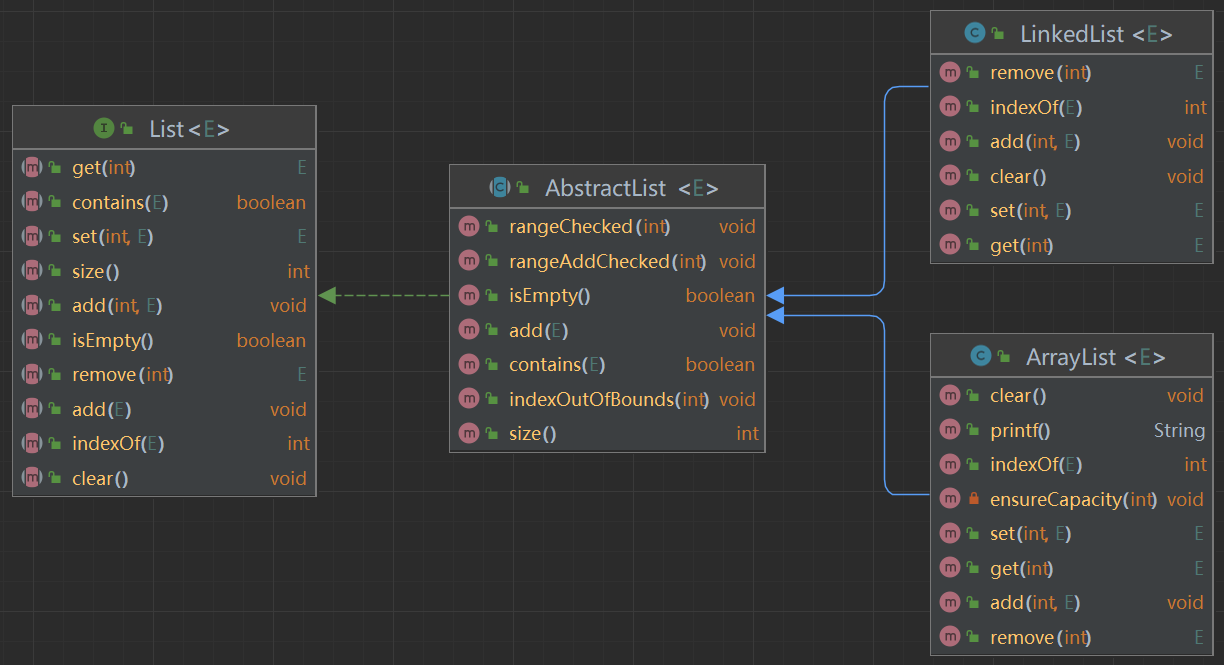
我们从动态数组中我们可以再次对 List 集合进行优化,我们将公共部分进行封装为 AbstractList 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public interface List<E> {
int size();
boolean isEmpty();
boolean contains(E element);
void add(E element);
E get(int index);
E set(int index, E element);
void add(int index, E element);
E remove(int index);
int indexOf(E element);
void clear();
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| public abstract class AbstractList<E> implements List<E> {
protected int size = 0;
@Override
public int size() { return size; }
@Override
public boolean isEmpty() { return size == 0; }
@Override
public boolean contains(E e) { return indexOf(e) >= 0; }
@Override
public void add(E element) { add(size, element);
public void rangeChecked(int index) { if (index >= size || index < 0) { indexOutOfBounds(index); } }
public void rangeAddChecked(int index) { if (index > size || index < 0) { indexOutOfBounds(index); } }
public void indexOutOfBounds(int index) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); }
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public class LinkedList<E> extends AbstractList<E> {
@Override
public E get(int index) {
return null;
}
@Override
public E set(int index, E element) {
return null;
}
@Override
public void add(int index, E element) { }
@Override
public E remove(int index) {
return null;
}
@Override
public int indexOf(E element) {
return 0;
}
@Override
public void clear() {}
}
|
4. 代码实现
4.1. 初始化
需求:实现双向链表的初始化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public class LinkedList<E> extends AbstractList<E> {
private Node<E> first;
private Node<E> last;
public static class Node<E> {
Node<E> prev;
E element;
Node<E> next;
public Node(Node<E> prev, E element, Node<E> next) {
this.prev = prev;
this.element = element;
this.next = next;
}
}
}
|
4.2. 获取节点
需求:通过 index 获取 node 节点。
实现步骤:
- 由于目前采取的双向链表,所以相对于可以根据具体的
size >> 1 进行查找。
- 首先,我们需要将
size >> 1 。
- 然后,根据
index 跟 size >> 1 进行判断,是从前驱节点还是后驱节点进行查找。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
private Node<E> node(int index) {
rangeChecked(index);
Node<E> node;
if ((size >> 1) > index) {
node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
} else {
node = last;
for (int i = size - 1; i > index; i--) {
node = node.prev;
}
}
return node;
}
|
4.3. 添加元素到指定位置
需求:我们需要将元素添加到指定位置。
注意:分别考虑将元素添加到中间、添加到第一索引位置、最后一个索引位置。
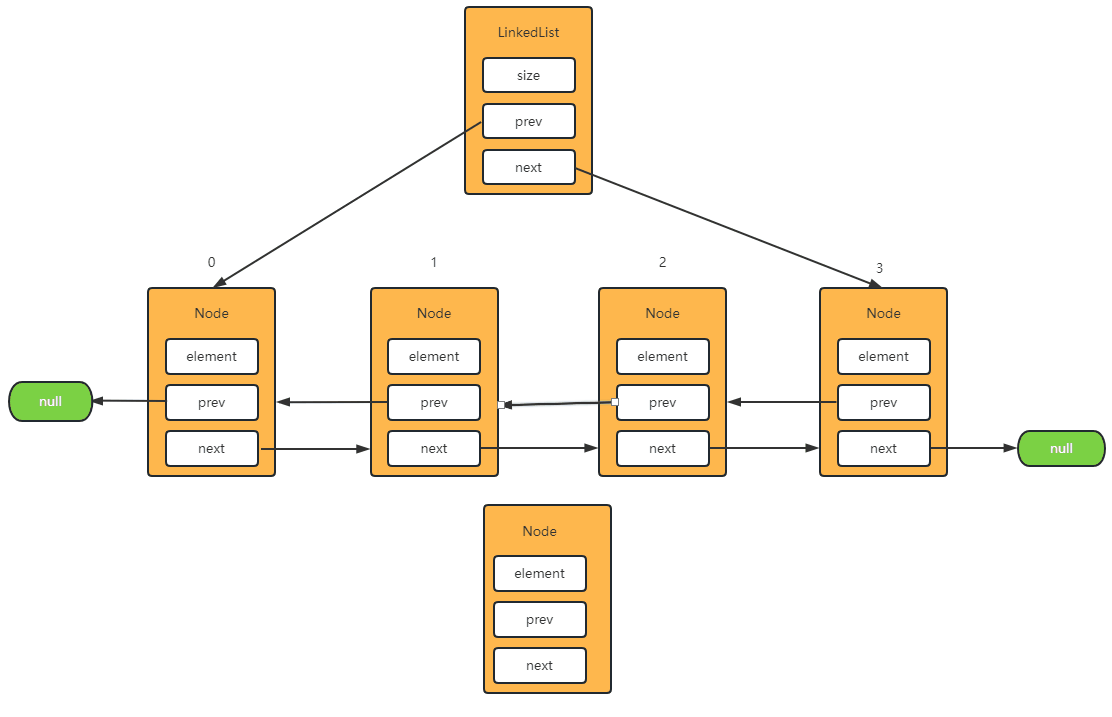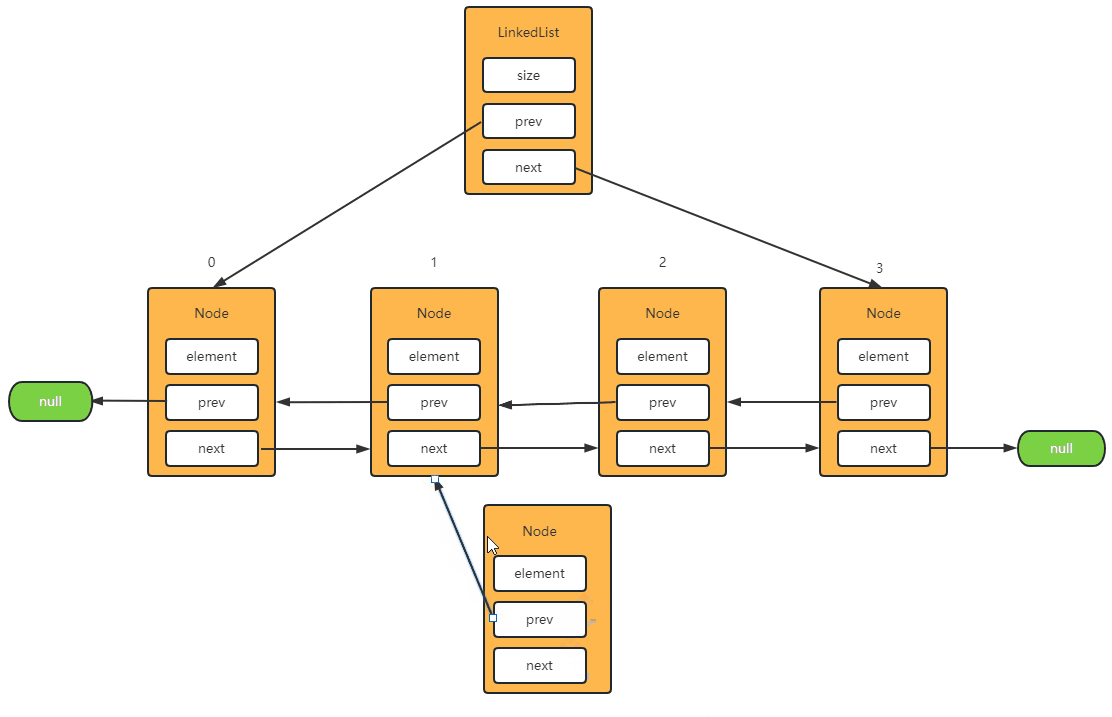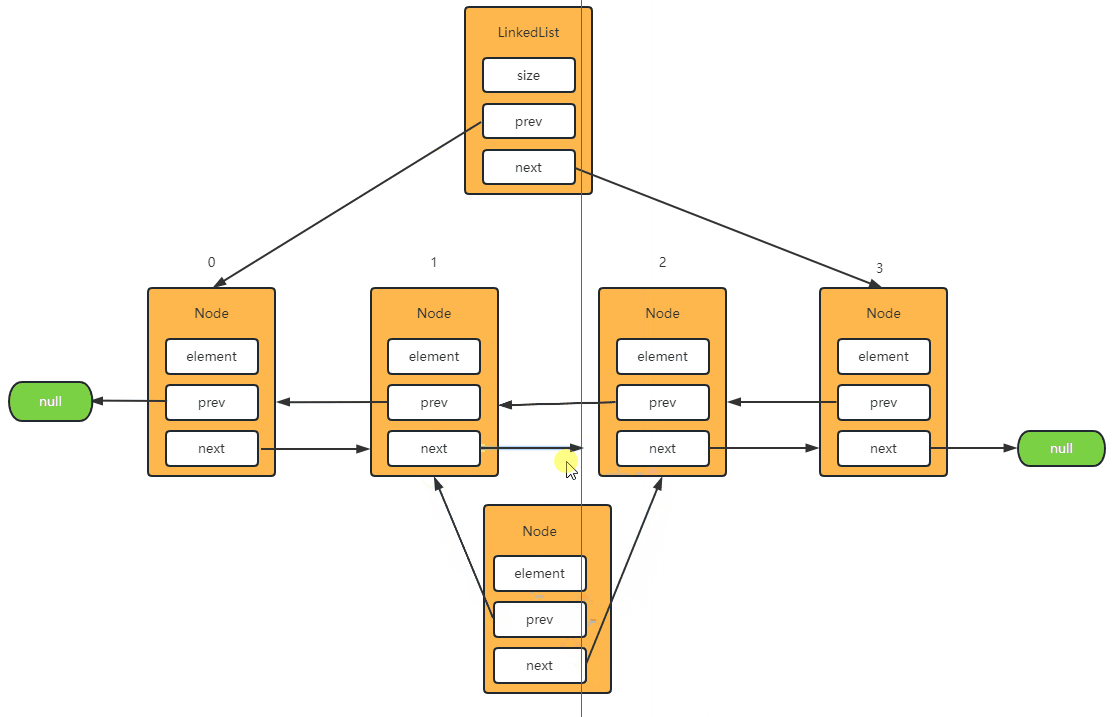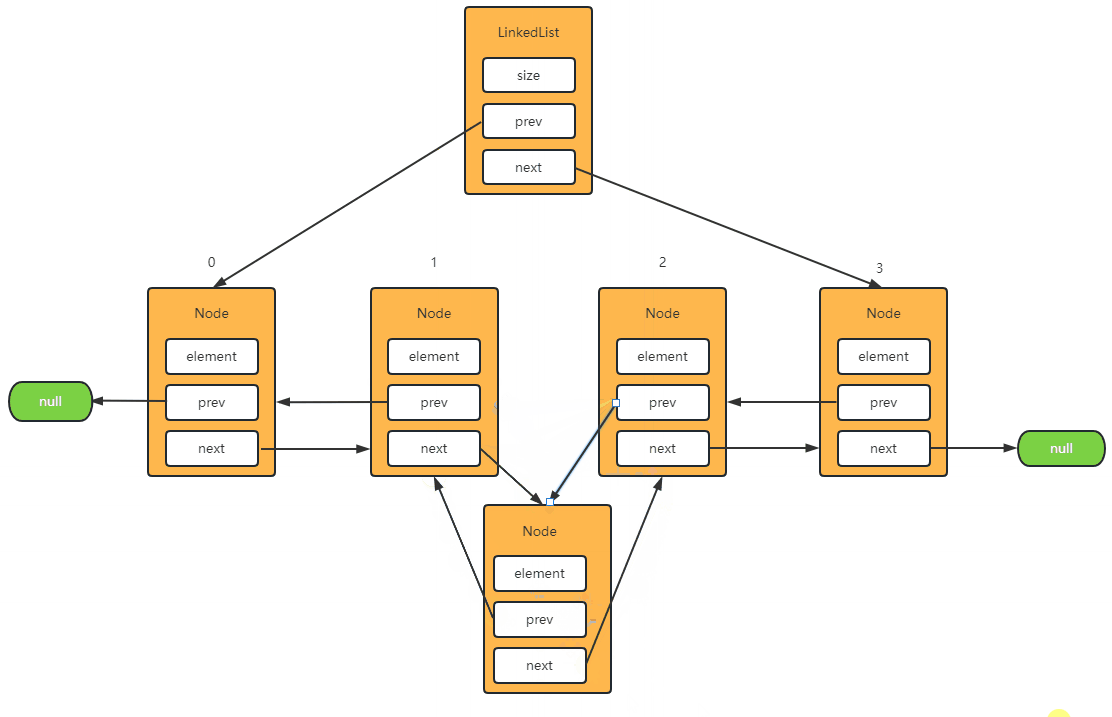
Step-1: 将元素添加到中间
- 首先,获取 index 索引的节点,并将前驱节点指向新节点。
- 然后,获取 index 索引节点的上一个节点,并将后驱节点指向新节点。
- 最后,将新节点的前后指针分别指向上面两个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
| @Override
public void add(int index, E element) {
rangeAddChecked(index);
Node<E> nextNode = node(index);
Node<E> prevNode = nextNode.prev;
Node<E> node = new Node<>(prevNode, element, nextNode);
prevNode.next = node;
nextNode.prev = node;
size++;
}
|
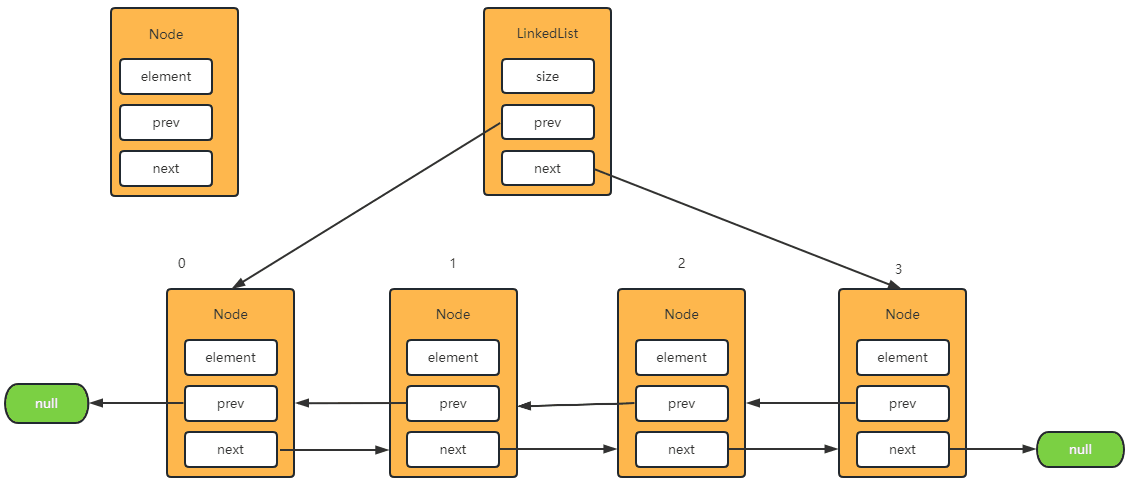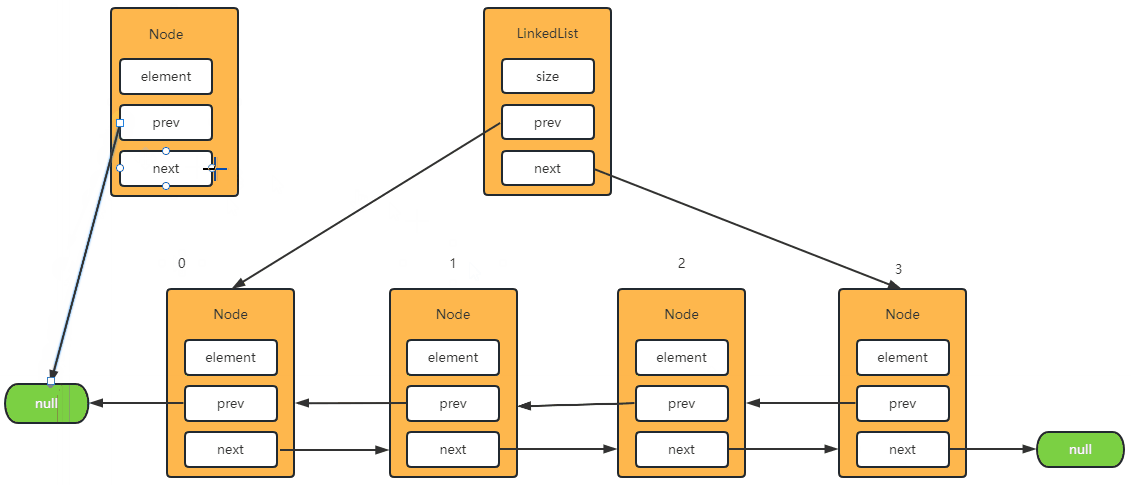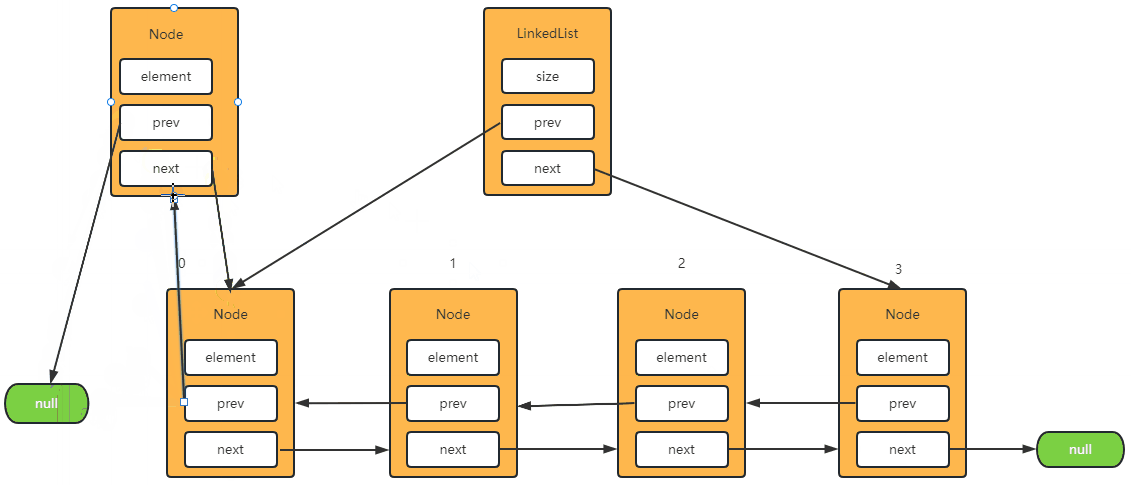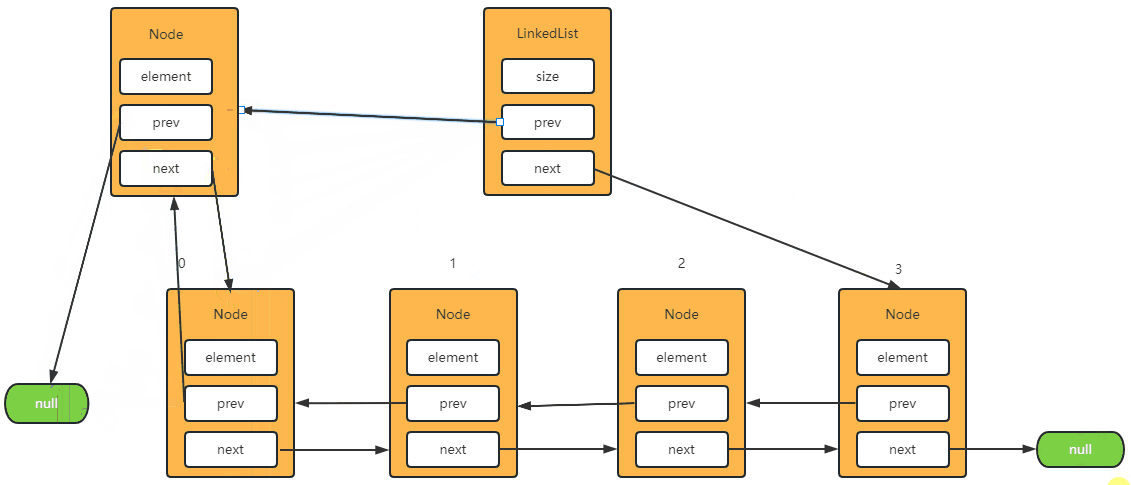
Step-2: 将元素添加到第一位
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| @Override
public void add(int index, E element) {
rangeAddChecked(index);
Node<E> nextNode = node(index);
Node<E> prevNode = nextNode.prev;
Node<E> node = new Node<>(prevNode, element, nextNode);
nextNode.prev = node;
if (prevNode == null) {
first = node;
} else {
prevNode.next = node;
}
size++;
}
|
Step-3: 将元素添加到最后一位
- 当
index == size 的时候就等于再往最后一个位置在添加元素了。
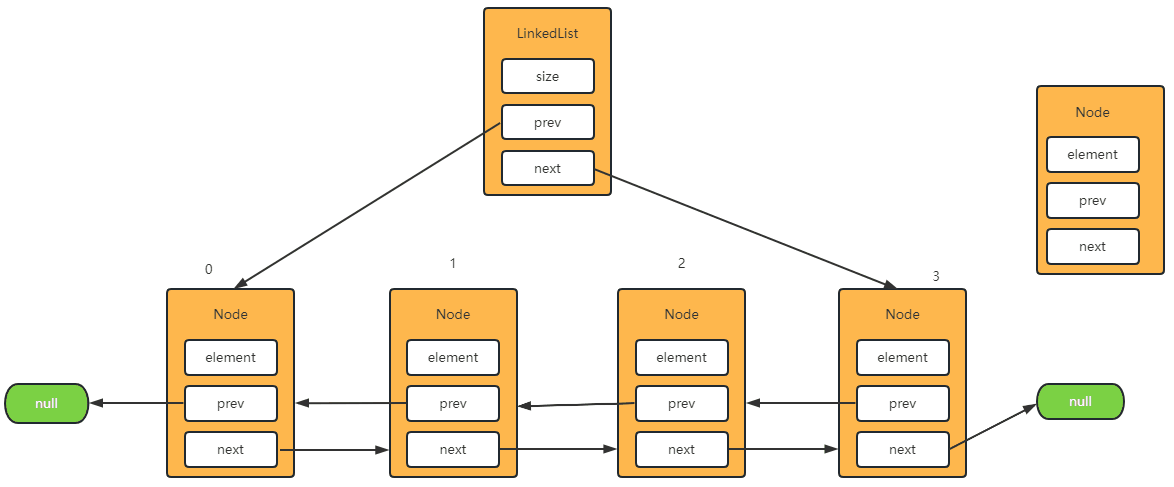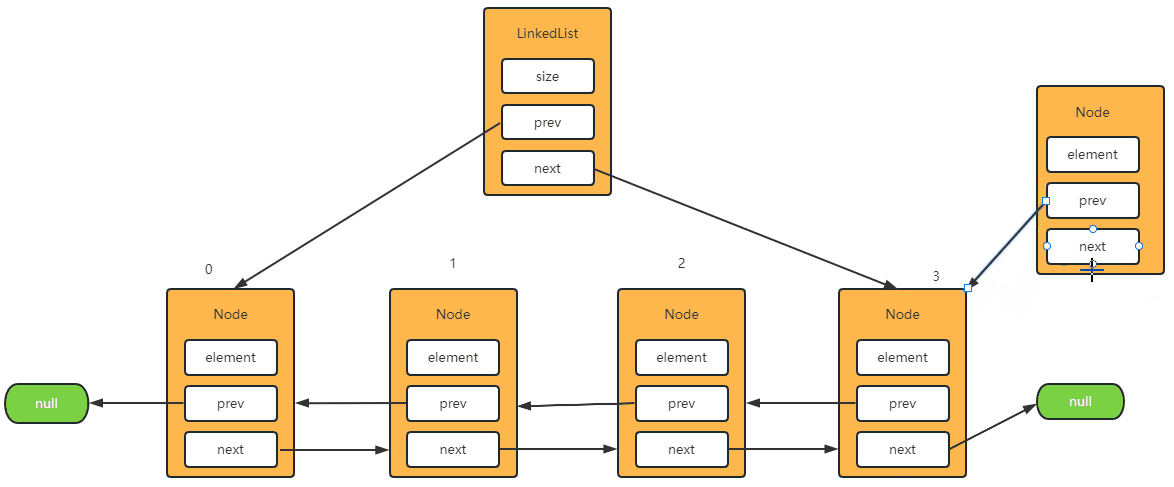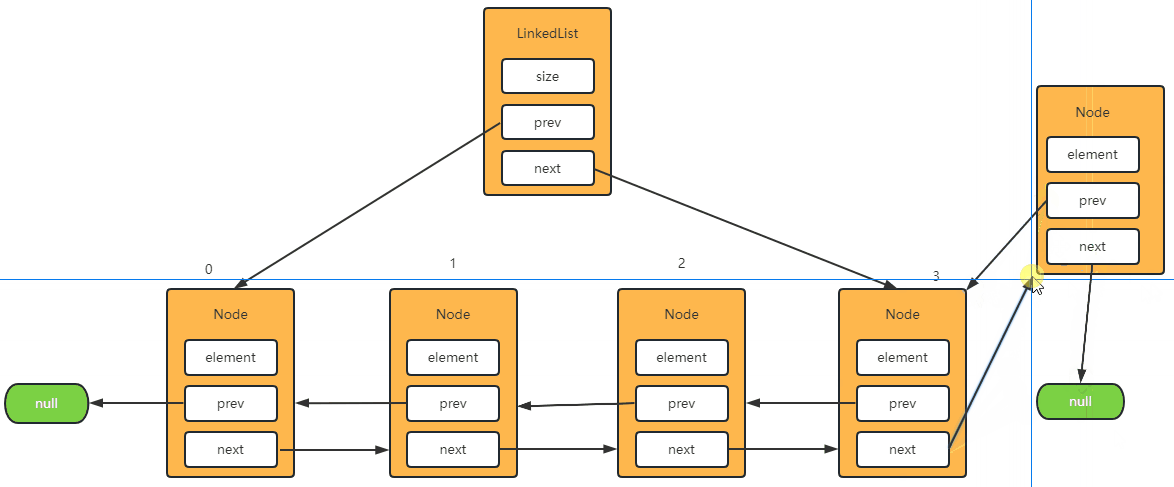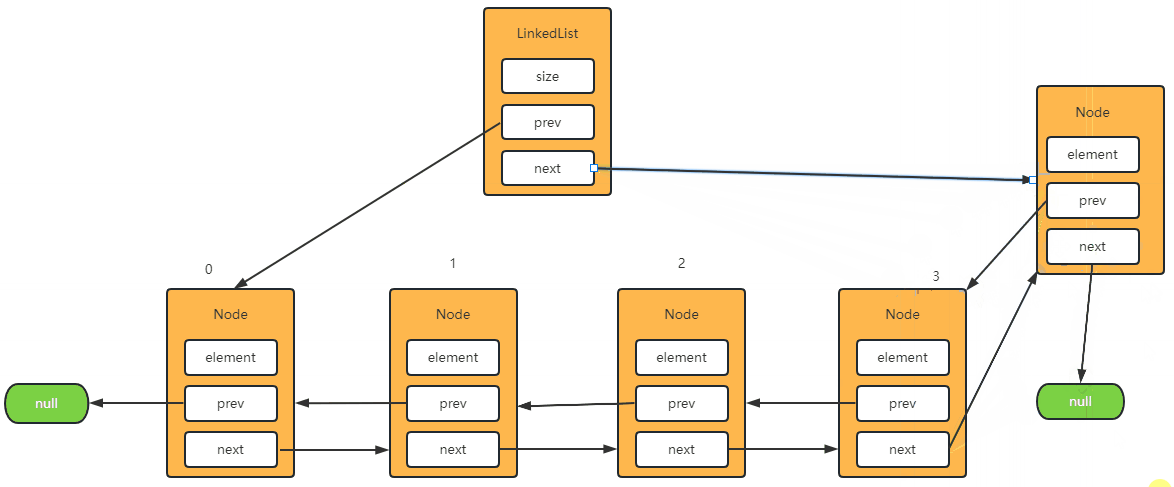
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| @Override
public void add(int index, E element) {
rangeAddChecked(index);
if (index == size) {
Node<E> nextNode = last;
Node<E> node = new Node<>(nextNode, element, null);
last = node;
nextNode.next = node;
} else {
Node<E> nextNode = node(index);
Node<E> prevNode = nextNode.prev;
Node<E> node = new Node<>(prevNode, element, nextNode);
nextNode.prev = node;
if (prevNode == null) {
first = node;
} else {
prevNode.next = node;
}
}
size++;
}
|
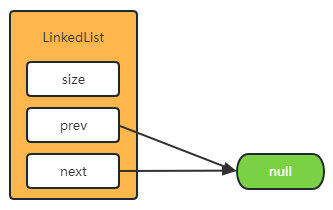
注意事项:如果 size 为 0 时,index == size 就会存在问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| @Override
public void add(int index, E element) {
rangeAddChecked(index);
if (index == size) {
Node<E> lastNode = last;
last = new Node<>(lastNode, element, null);
if (lastNode == null) {
first = last;
} else {
lastNode.next = last;
}
} else {
Node<E> nextNode = node(index);
Node<E> prevNode = nextNode.prev;
Node<E> node = new Node<>(prevNode, element, nextNode);
nextNode.prev = node;
if (prevNode == null) {
first = node;
} else {
prevNode.next = node;
}
}
size++;
}
|
4.4. 删除指定元素
需求:设置指定元素。
注意事项:需要考虑删除删除中间节点,第一个节点,最后一个节点。
删除中间节点
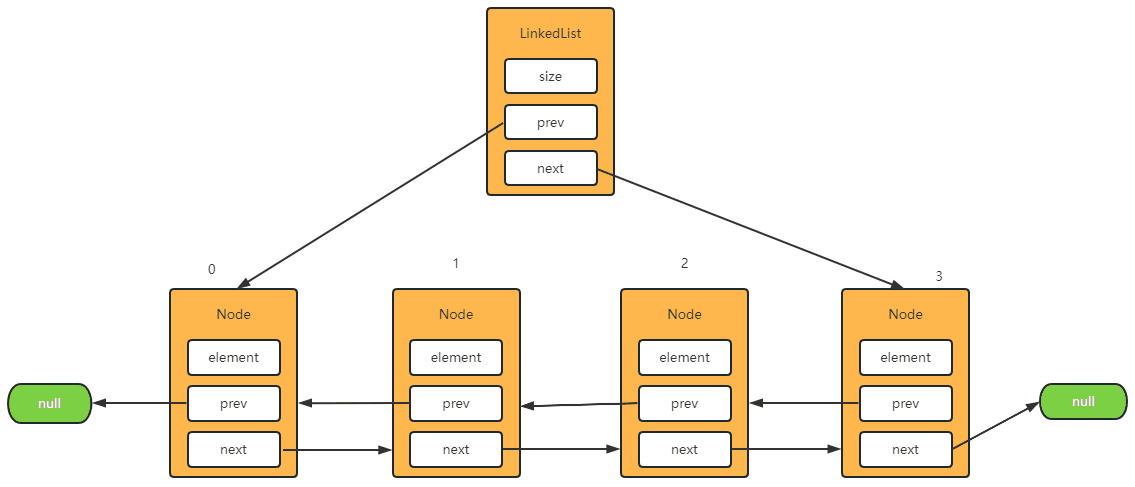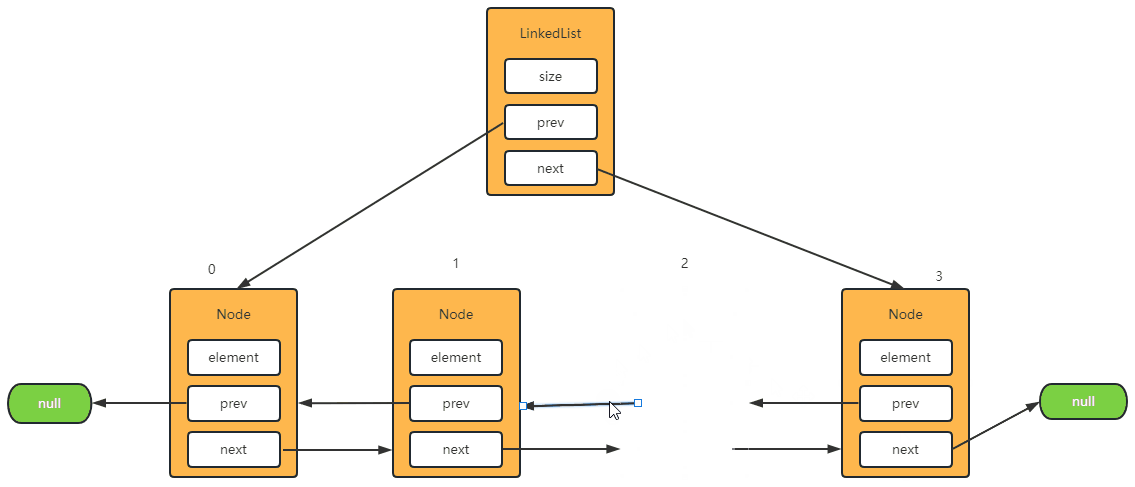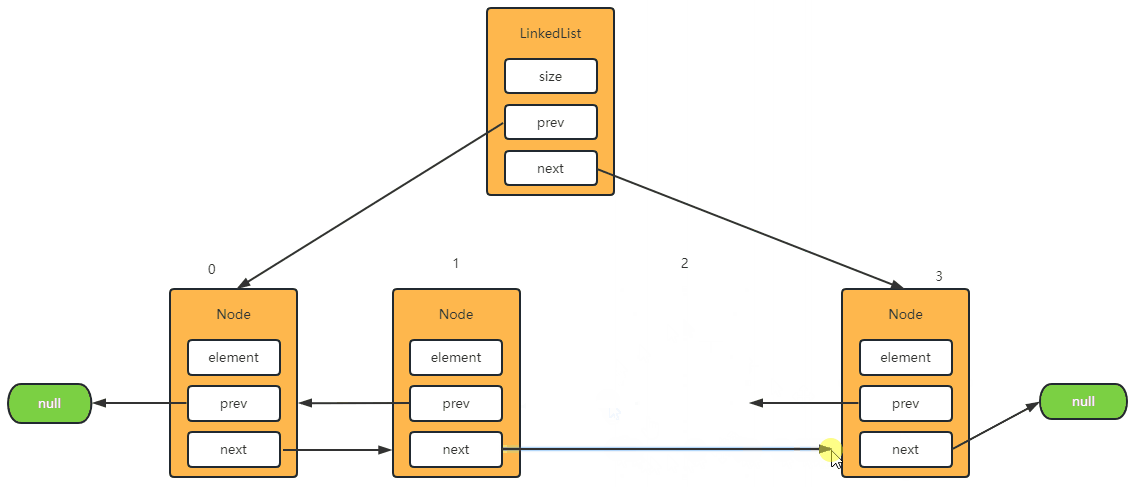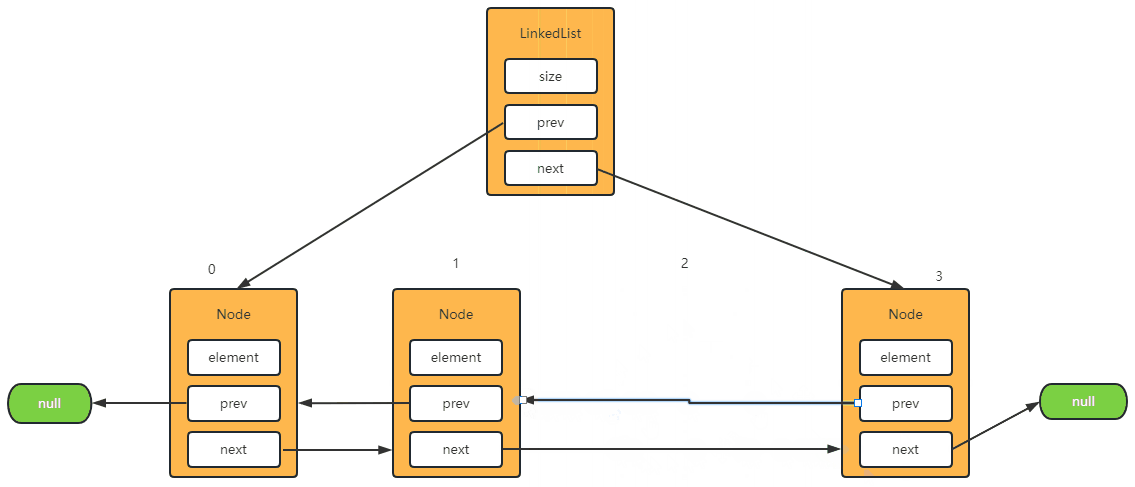
1
2
3
4
5
6
7
8
9
10
11
12
13
| @Override
public E remove(int index) {
rangeChecked(index);
Node<E> node = node(index);
Node<E> prevNode = node.prev;
Node<E> nextNode = node.next;
prevNode.next = nextNode;
nextNode.prev = prevNode;
size--;
return node.element;
}
|
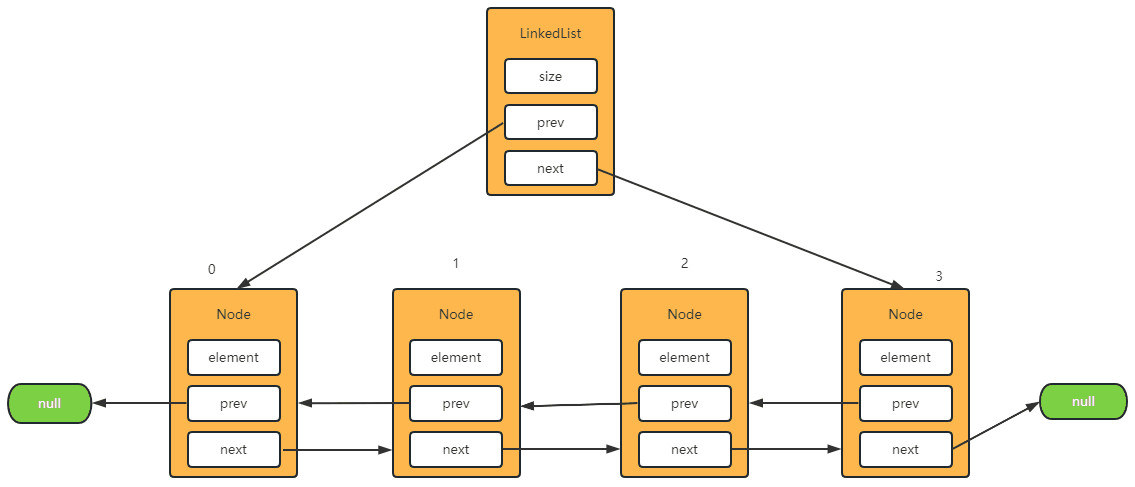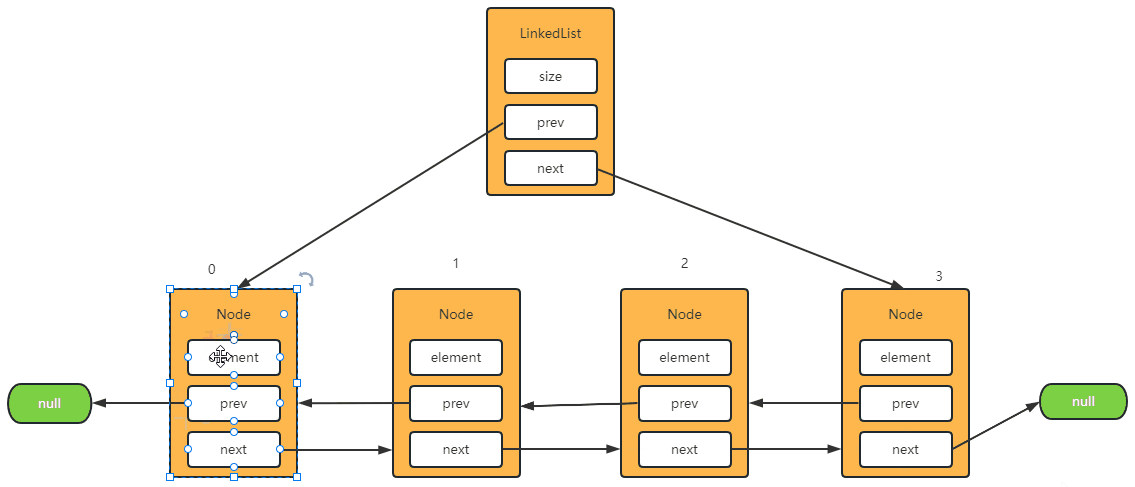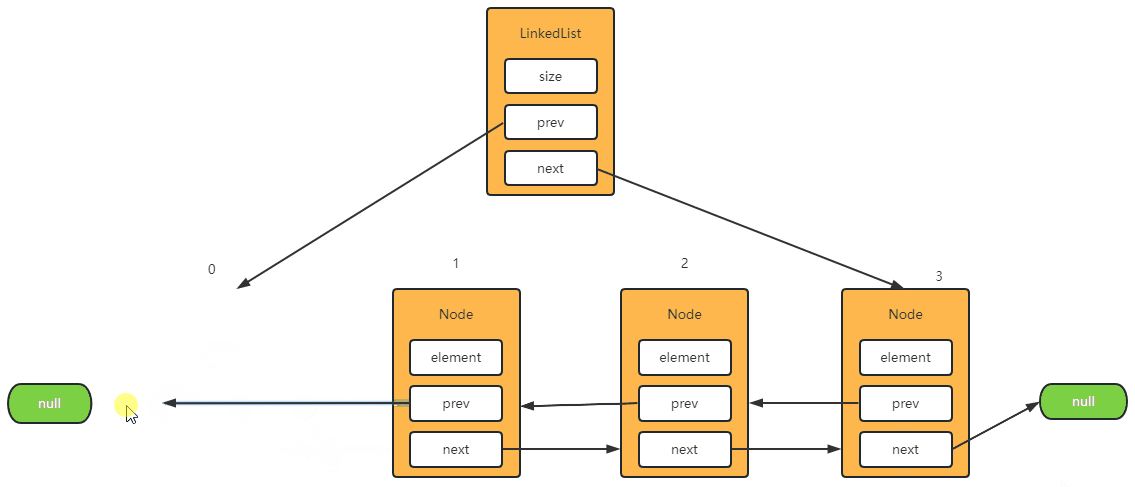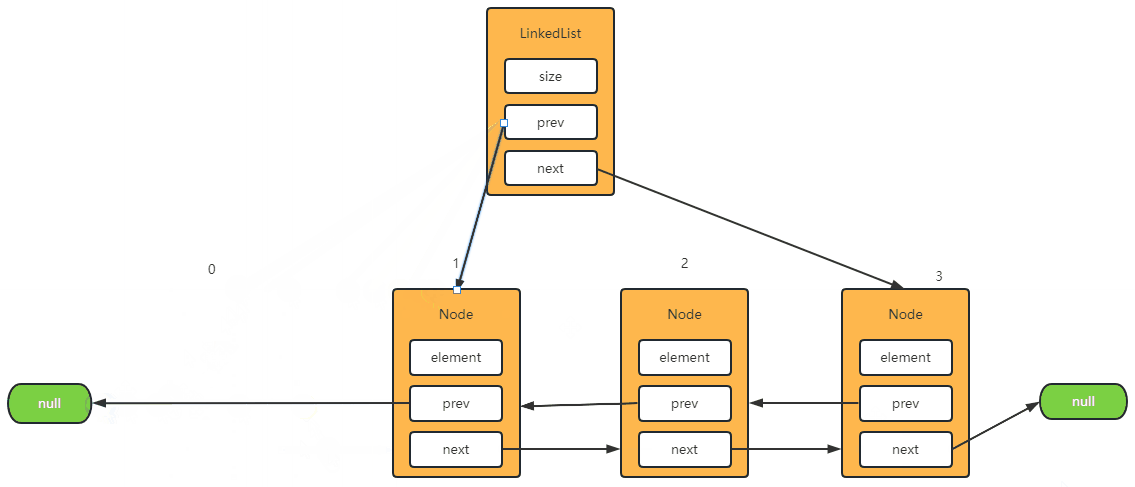
Step-1: 删除第一个元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
@Override
public E remove(int index) {
rangeChecked(index);
Node<E> node = node(index);
Node<E> prevNode = node.prev;
Node<E> nextNode = node.next;
nextNode.prev = prevNode;
if (prevNode == null) {
first = nextNode;
} else {
prevNode.next = nextNode;
}
size--;
return node.element;
}
|
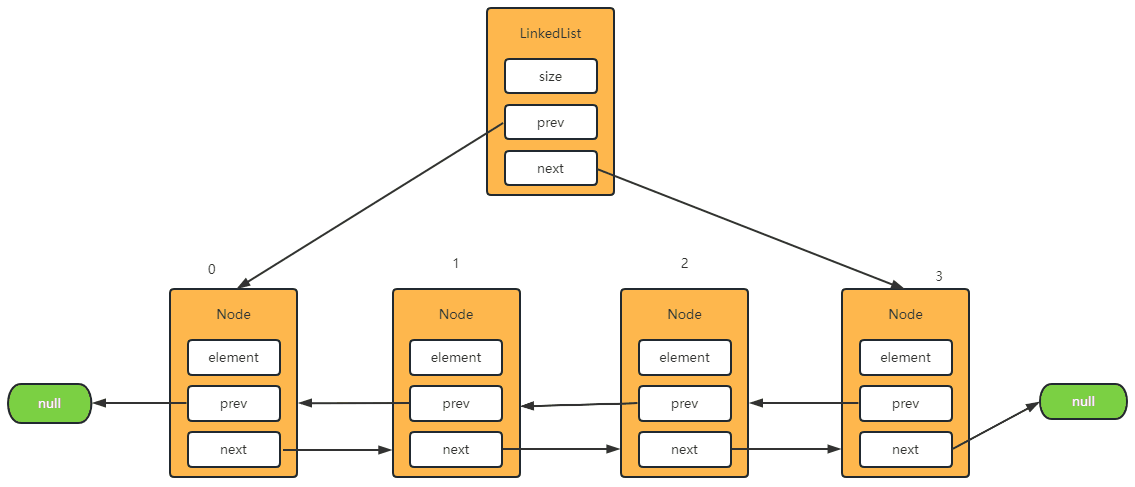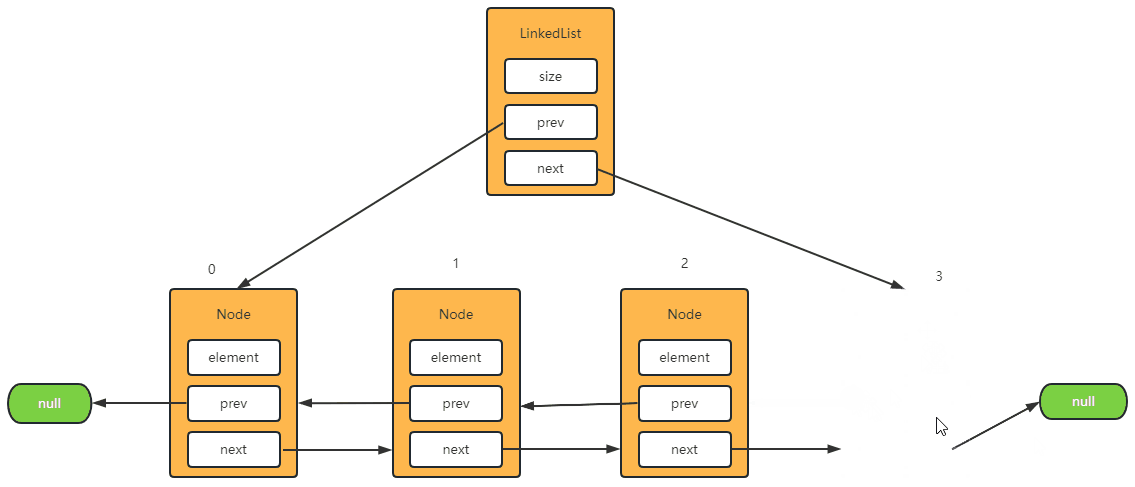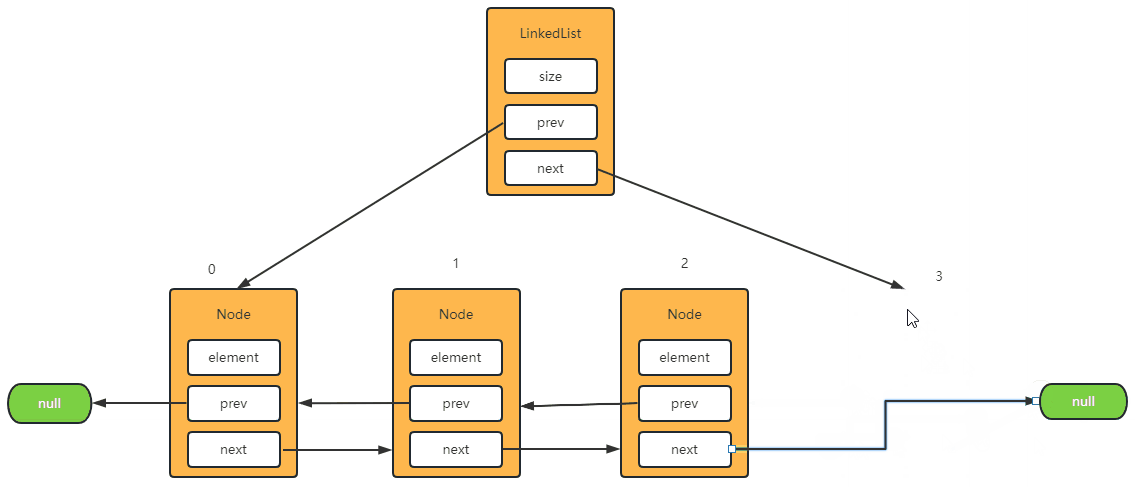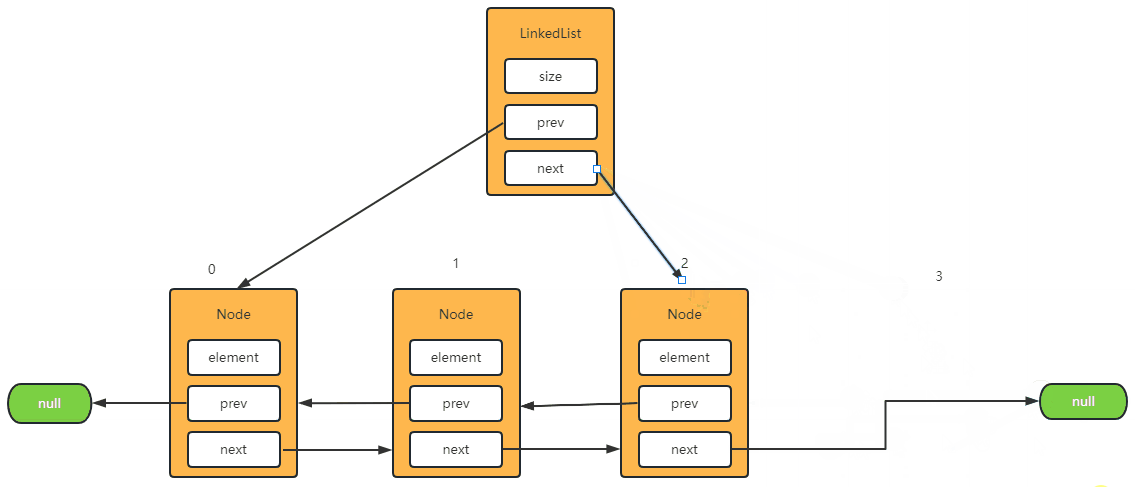
Step-2: 删除最后一个元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
@Override
public E remove(int index) {
rangeChecked(index);
Node<E> node = node(index);
Node<E> prevNode = node.prev;
Node<E> nextNode = node.next;
if (nextNode == null) {
last = prevNode;
} else {
nextNode.prev = prevNode;
}
if (prevNode == null) {
first = nextNode;
} else {
prevNode.next = nextNode;
}
size--;
return node.element;
}
|
4.5. 设置指定位置元素
需求:设置指定位置元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
@Override
public E set(int index, E element) {
Node<E> node = node(index);
E oldElement = node.element;
node.element = element;
return oldElement;
}
|
4.6. 清空元素
需求:清空节点所有元素。
1
2
3
4
5
6
7
8
9
|
@Override
public void clear() {
size = 0;
first = null;
last = null;
}
|
4.7. 获取指定位置元素
需求:根据所有获取到当前节点,然后在获取节点的 element。
1
2
3
4
5
6
7
8
9
10
|
@Override
public E get(int index) {
return node(index).element;
}
|
4.8. 获取元素索引
需求:获取元素索引。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
@Override
public int indexOf(E element) {
Node<E> node = first;
if (element == null) {
for (int i = 0; i < size; i++) {
if (node.element == null) {
return i;
}
node = node.next;
}
} else {
for (int i = 0; i < size; i++) {
if (element.equals(node.element)) {
return i;
}
node = node.next;
}
}
return -1;
}
|
4.9. 打印元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("{ size = ").append(size).append(" , Node = [ ");
Node<E> node = first;
for (int i = 0; i < size; i++) {
if (i != 0) {
builder.append(",");
}
builder.append(node.element);
node = node.next;
}
builder.append(" ]}");
return builder.toString();
}
|
4.10. 测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| public class LinkedListTest {
@Test
public void testAddAndGet() {
LinkedList<Integer> linkedList = new LinkedList<>();
linkedList.add(0, 1);
linkedList.add(1, 2);
linkedList.add(2, 3);
assertEquals((Object) 1, linkedList.get(0));
assertEquals((Object) 2, linkedList.get(1));
assertEquals((Object) 3, linkedList.get(2));
System.out.println("linkedList ===> " + linkedList);
}
@Test
public void testSet() {
LinkedList<String> linkedList = new LinkedList<>();
linkedList.add(0, "apple");
linkedList.add(1, "banana");
assertEquals("apple", linkedList.set(0, "orange"));
assertEquals("orange", linkedList.get(0));
System.out.println("linkedList ===> " + linkedList);
}
@Test
public void testRemove() {
LinkedList<Character> linkedList = new LinkedList<>();
linkedList.add(0, 'a');
linkedList.add(1, 'b');
linkedList.add(2, 'c');
assertEquals('b', (char) linkedList.remove(1));
assertEquals("{ size = 2 , Node = [ a,c ]}", linkedList.toString());
}
@Test
public void testIndexOf() {
LinkedList<Integer> linkedList = new LinkedList<>();
linkedList.add(0, 10);
linkedList.add(1, 20);
linkedList.add(2, 30);
assertEquals(1, linkedList.indexOf(20));
assertEquals(-1, linkedList.indexOf(40));
}
@Test
public void testClear() {
LinkedList<String> linkedList = new LinkedList<>();
linkedList.add(0, "one");
linkedList.add(1, "two");
linkedList.clear();
assertEquals("{ size = 0 , Node = [ ]}", linkedList.toString());
}
}
|
5. 总结
5.1. 双向链表 VS 单向链表
- 单项链表:单项链表主要解决了内存空间的浪费,也是在数组的基础上进行了一个优化。
- 双向链表:作为单向链表的升级版,查询的速度减半了,可以根据索引的大小进行判断是从前驱节点还是后驱节点进行查找,新增了一个节点元素。
5.2. 双向链表 VS 动态数组
| 数据结构 |
优点 |
缺点 |
适用场景 |
| 动态数组 |
开辟、销毁内存空间次数相对较少 |
可能造成内存浪费(可缩容解决) |
1. 频繁尾部操作
2. 快速查询(随机访问) |
| 双向链表 |
不会造成内存空间的浪费 |
开辟、销毁内存空间的次数相对较多 |
1. 频繁头部操作
2. 任意位置快速操作 |
6. 参考博文
















