数据结构-B树
1. 内容大纲
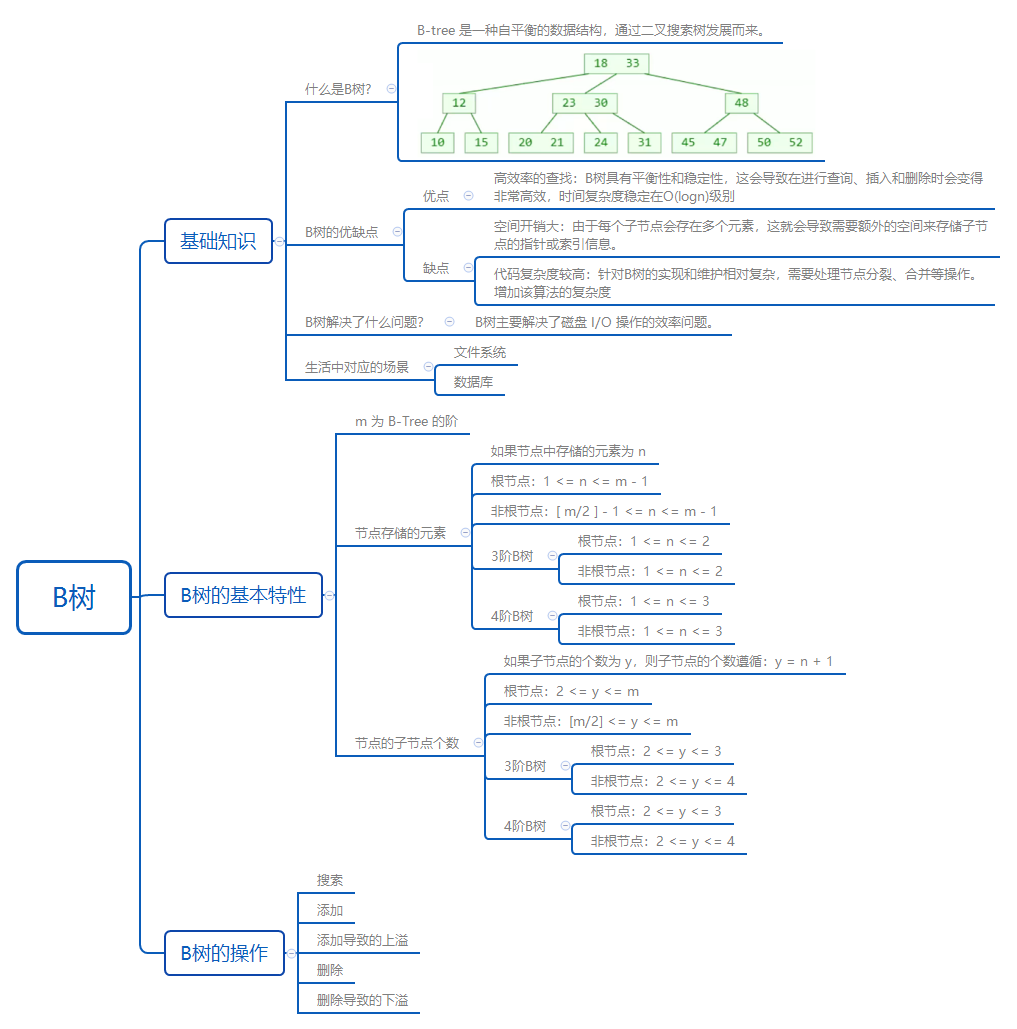
2. 基础知识
2.1. 什么是B树?
B-Tree 是一种自平衡的树形结构,通过二叉搜索树发展而来。
B-Tree 中一个节点中可以存储多个元素,一个
B-Tree中某个节点存在最多的子节点我们称为几阶B-Tree。B-Tree 可以分为
3阶B树、4阶B树、5阶B树等等,具体如下图: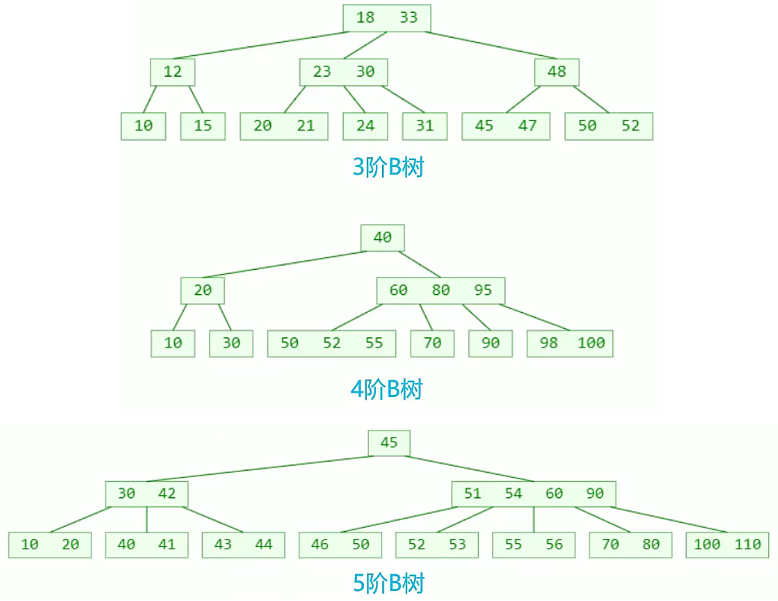
2.2. B树的优缺点
优点
- 高效的操作:B-Tree 在查找、添加、删除时可以将时间复杂度维护在
O(logn)级别。因为B-Tree是基于平衡二叉搜索树,这也就导致了B-Tree平衡性和稳定性。
缺点
空间开销会增大:由于每个节点中可能会存在多个元素,这就导致需要额外的空间来存储子节点的索引信息。
代码复杂度较高:针对 B树 的实现和维护可能相对复杂,因为在节点添加时会导致节点上溢、合并等操作。
2.3. B树解决了什么问题?
二叉搜索树
- 在传统的二叉搜索树中,数据分布在不同的块或页中。这就意味着,在进行插入或查找操作时,频繁的磁盘读取或写入会不可避免地发生。这种I/O操作频繁性会直接影响系统性能,成为系统的瓶颈。
B树主要解决了磁盘
I/O的问题- B-Tree中由于一个节点中存储了多个元素,使得每个节点中的大小与磁盘块大小相近。这就意味着每次读取或者写入磁盘时,可以高效利用磁盘
I/O。 - B-Tree中保持了平衡二叉树的平衡性,这也会导致二叉树的高度较低,从根节点到叶子节点的路径较短,可以更快的锁定目标数据在磁盘页或块中,减少磁盘的
I/O操作。
- B-Tree中由于一个节点中存储了多个元素,使得每个节点中的大小与磁盘块大小相近。这就意味着每次读取或者写入磁盘时,可以高效利用磁盘
2.4. 生活中对应的场景
满足
B-Tree特性需要保证数据量足够大和频繁的对数据进行操作数据库中就应用到了
B-Tree的特性- 文件系统也应用到了
B-Tree的特性
3. B树的基本特性(重要)
一个元素的子节点元素最大的度,我们称为m阶B树。

- 如果一个节点中存储的元素为
n,则有如下规则:- 根节点:1 <= n <= m - 1
- 例如:3阶B树的根节点最多为 1 <= n <= 2,即 根节点存储的元素的范围为 [ 1, 2 ]
- 例如:4阶B树的根节点最多为 1 <= n <= 3,即 根节点存储的元素的范围为 [ 1, 3 ]
- 非根节点:[ m/2 ] - 1 <= n <= m - 1。其中 [ m/2 ] 会进行向上取整,例如 [ 3 / 2 ] = 2
- 例如:3阶B树的非根节点最多为 1 <= n <= 2,即 非根节点存储的元素的范围为 [ 1, 2 ]
- 例如:4阶B树的非根节点最多为 1 <= n <= 3,即 非根节点存储的元素的范围为 [ 1, 3 ]
- 根节点:1 <= n <= m - 1
- 如果存在子节点,则子节点存在如下规则:
- 子节点的个数:
y = n + 1 - 根节点的子节点个数为:
2 <= y <= m- 例如:3阶B树的根节点的子节点个数的范围为
2 <= y <= 3,3阶B树的根节点的子节点的个数为 [ 2, 3 ] - 例如:4阶B树的根节点的子节点个数的范围为
2 <= y <= 4,4阶B树的根节点的子节点的个数为 [ 2, 4 ]
- 例如:3阶B树的根节点的子节点个数的范围为
- 非根节点的子节点个数为:
[m/2] <= y <= m,其中 [ m/2 ] 会进行向上取整,例如 [ 3 / 2 ] = 2- 例如:3阶B树的非根节点的子节点个数的范围为
2 <= y <= 3, 3阶B树的非根节点的子节点的个数为 [ 2, 3 ] - 例如:4阶B树的非根节点的子节点个数的范围为
2 <= y <= 4, 4阶B树的非根节点的子节点的个数为 [ 2, 4 ]
- 例如:3阶B树的非根节点的子节点个数的范围为
- 子节点的个数:
4. B树的操作
4.1. 搜索
如下图中,我们在 3 阶 B 树中进行搜索元素,具体流程如下图:
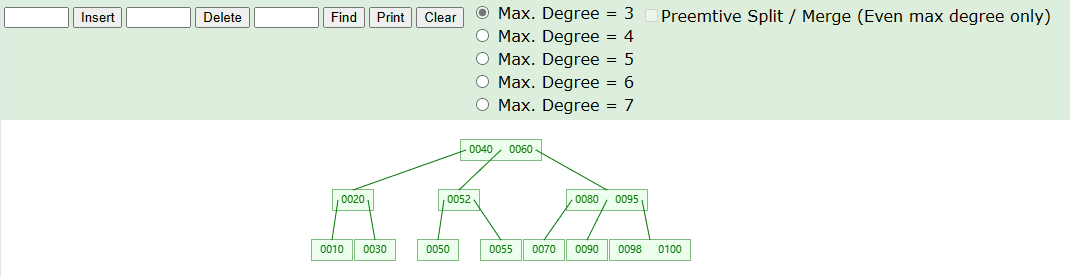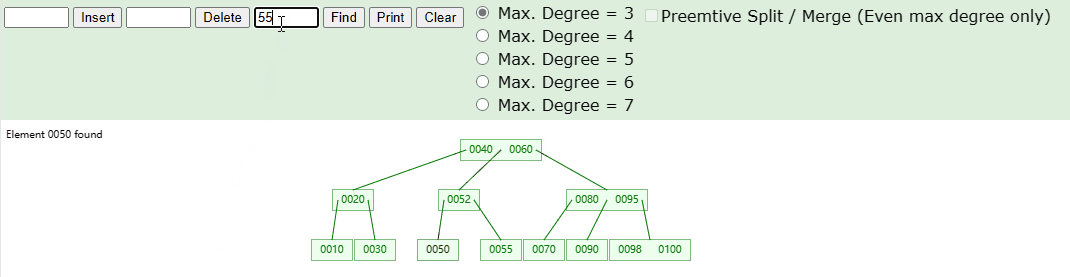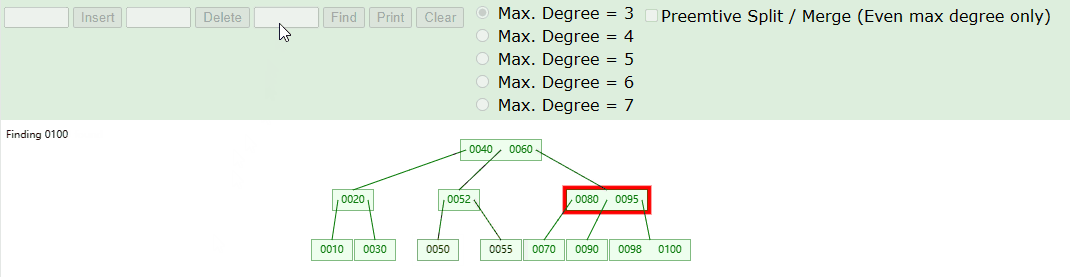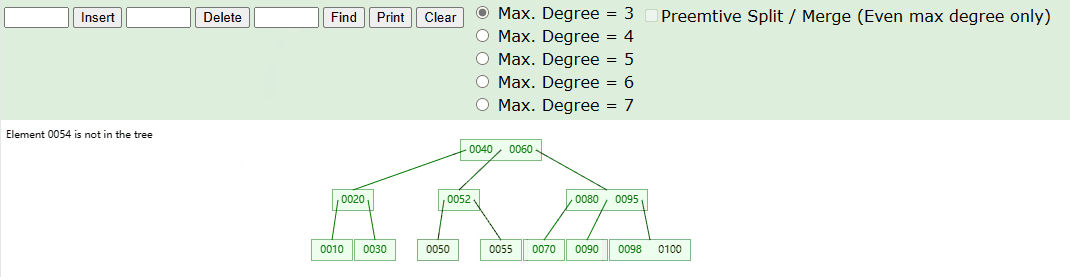
实现思路如下:
- Step-1:首先,我们从根节点元素进行,从大到小在节点内部进行遍历查找。
- Step-2:然后,如果命中就结束查找。
- Step-3:最后,如果未命中就在去对应的节点中进行查找,重复
Step-1的操作。
4.2. 添加
如下图中,我们在 3 阶 B 树中进行添加 51、54 元素,具体流程如下图:
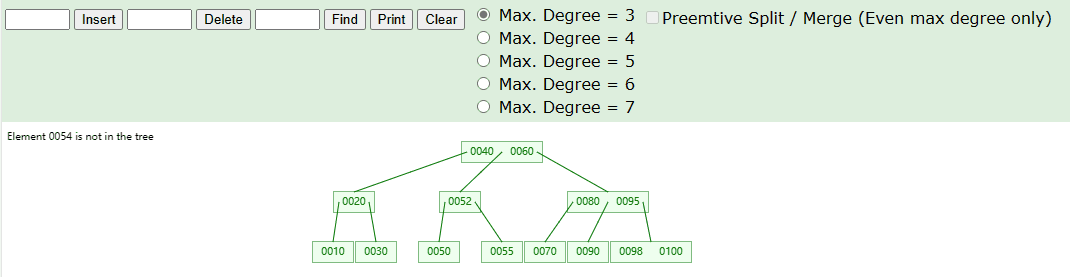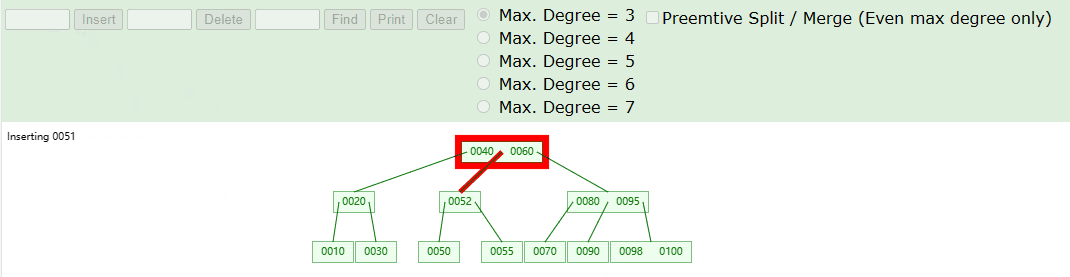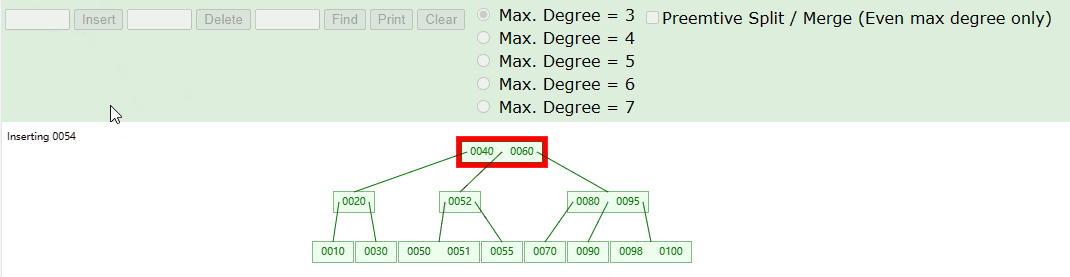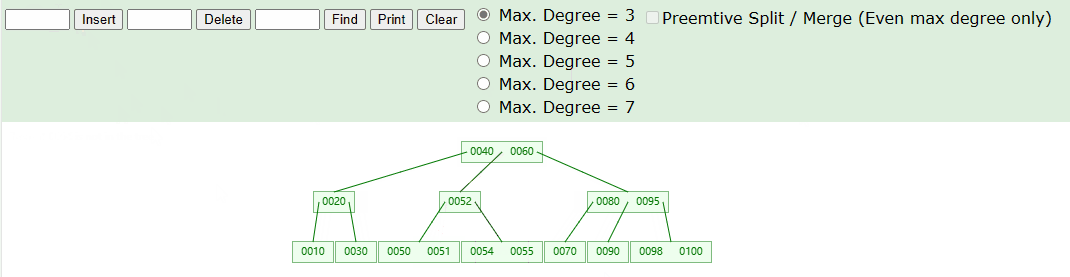
实现思路如下:
- Step-1:首先,我们查找当前需要添加元素的位置,由于 B-Tree 也是遵循二叉树的原则,也是遵循从左到右进行查找。
- Step-2:然后,找到添加元素的位置之后判断节点的大小,如果大于则添加到元素右边,小于则添加到元素左边。
- Step-3:最后,添加元素,更新元素数量。
4.3. 添加导致的上溢
由于刚才添加的元素是正常情况,没有导致元素上溢。但根据 3阶B树 的原则,非根节点元素不能超过2,如下我们添加元素 99 的情况就会导致元素上溢:
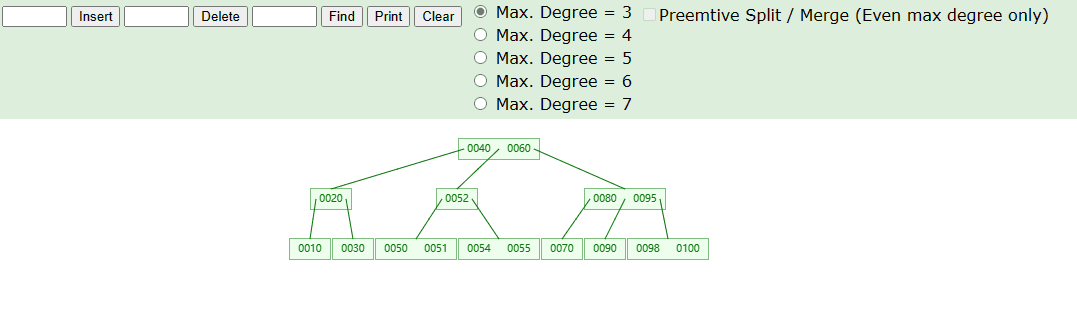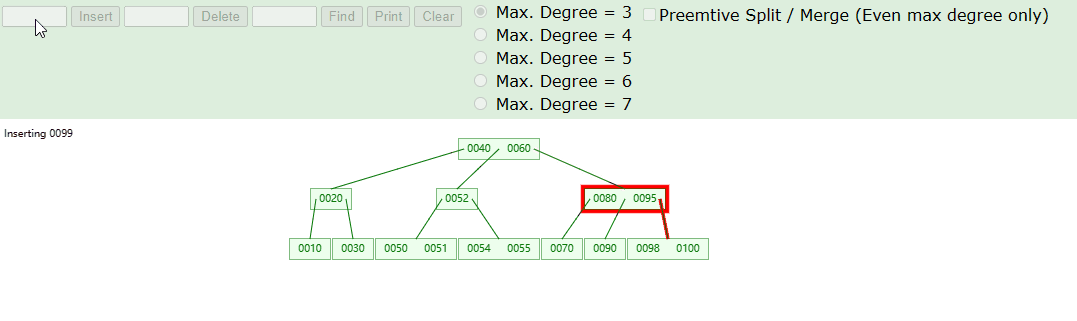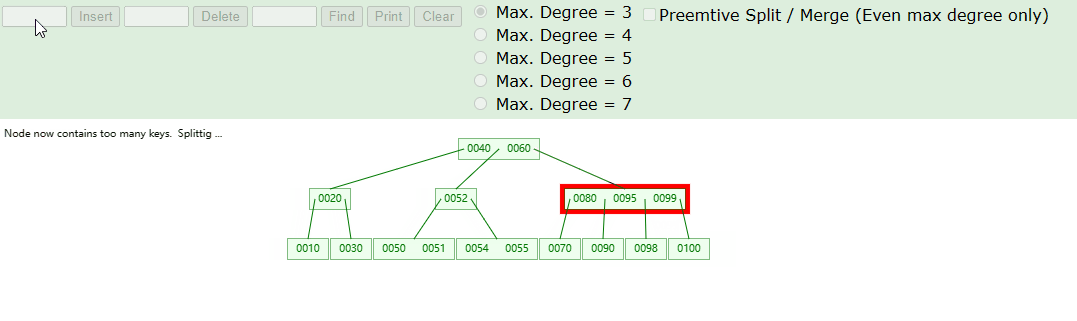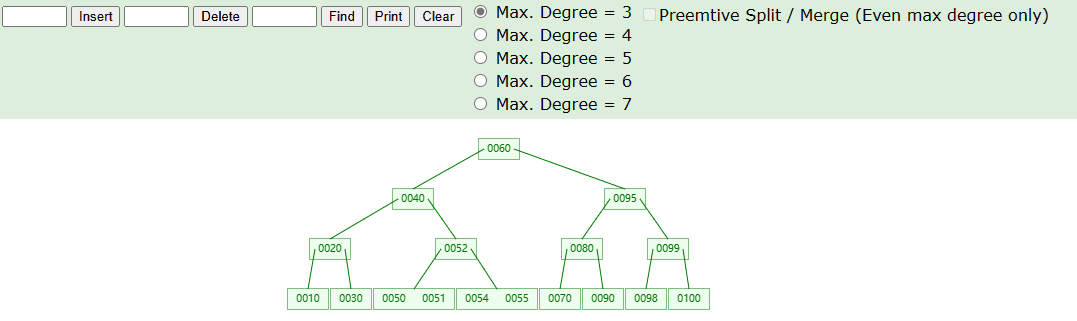
实现思路如下:
- Step-1:首先,将新添加的节点添加到对应的叶子节点时,如果一个节点已经满了,节点的元素数量达到了上限,这个时候就会上溢。
- Step-2:然后,找到当前节点的中间元素,进行向上分裂。
- Step-3:最后,如果上面节点也出现这个问题,则继续向上分裂。
4.4. 删除
删除叶子节点,具体操作如下图
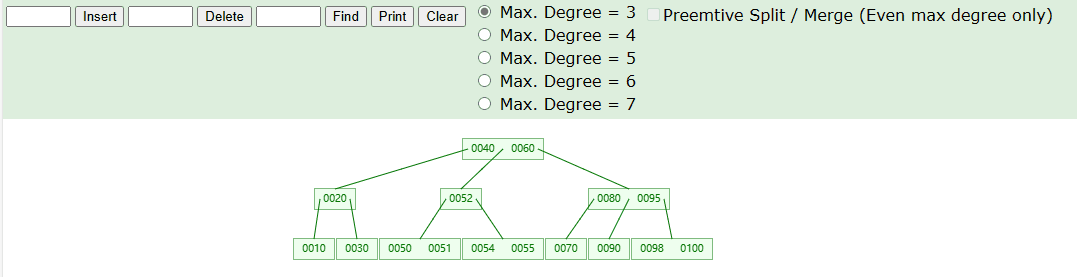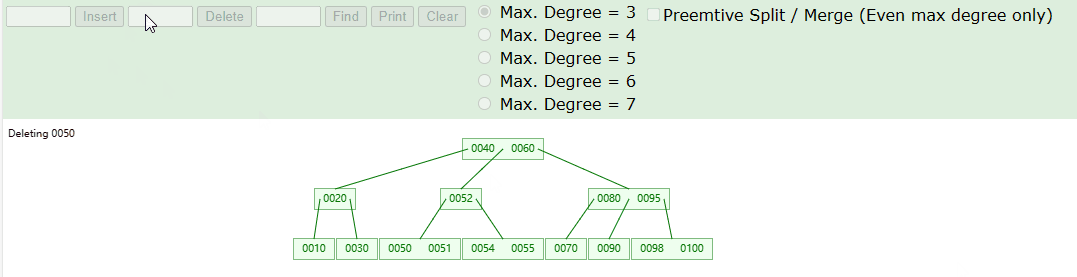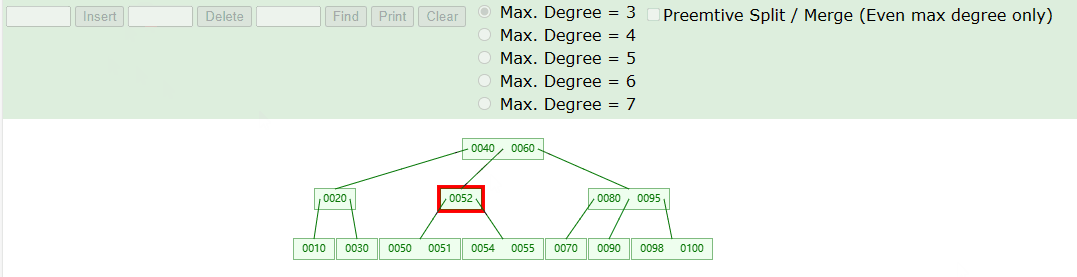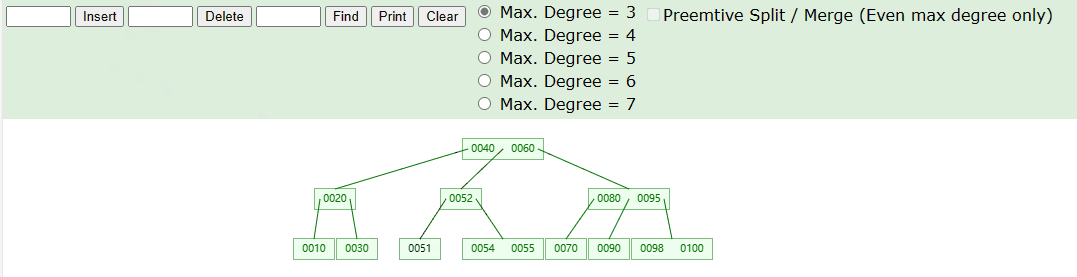
删除非叶子节点,具体操作如下图
- 针对删除非叶子节点,我们只需要找到对应的前驱或者后继节点,将删除的元素进行覆盖,再把前驱或者后继节点删除即可。
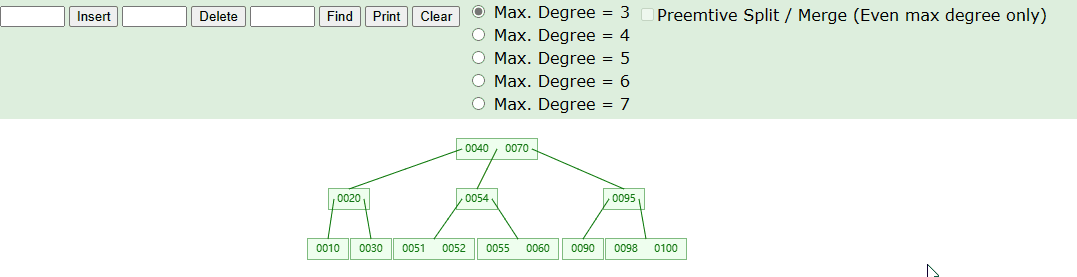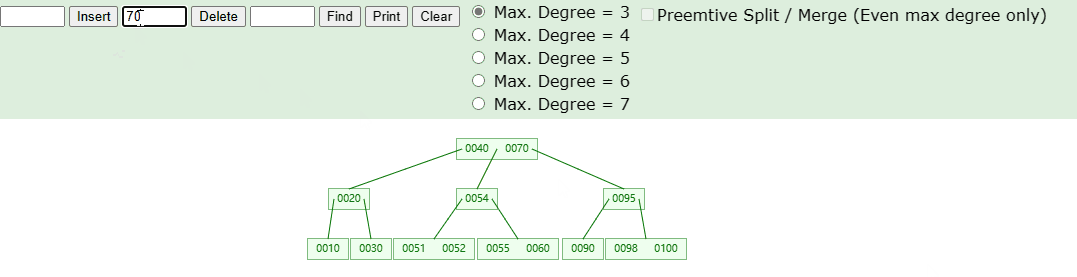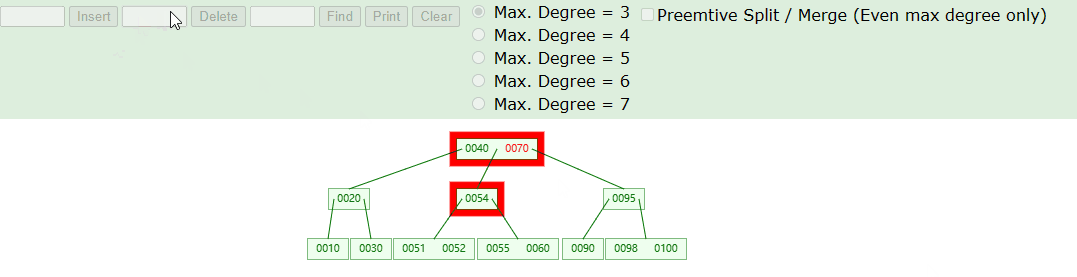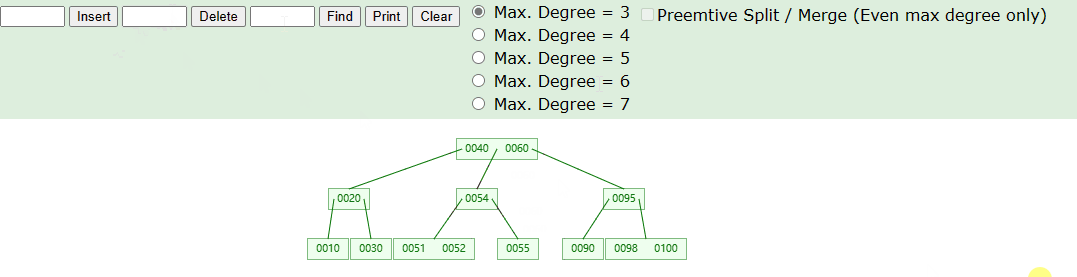
4.5. 删除导致的下溢
遵循3阶B树的特性,节点存储的元素和子节点个数遵循如下原则:
- 3阶B树节点存储的元素
- 根节点:1 <= n <= 2,[ 1, 2 ]
- 非根节点:1 <= n <= 2,[ 1, 2 ]
- 3阶B树子节点个数
- 根节点:2 <= y <= 3,[ 2, 3 ]
- 非根节点:2 <= y <= 4,[ 2, 4 ]
- 如下我们删除节点 90 ,就导致了B树的下溢。
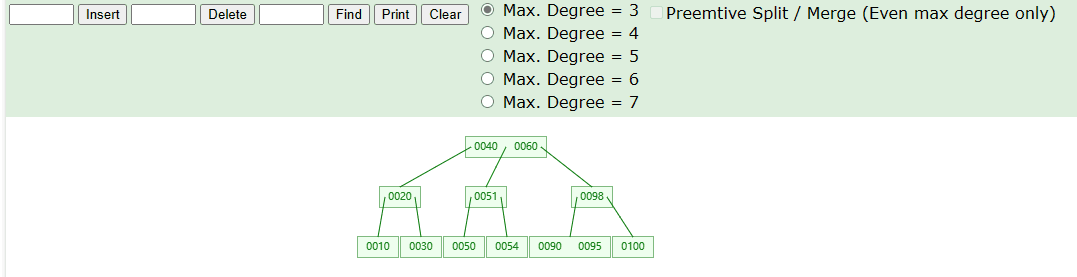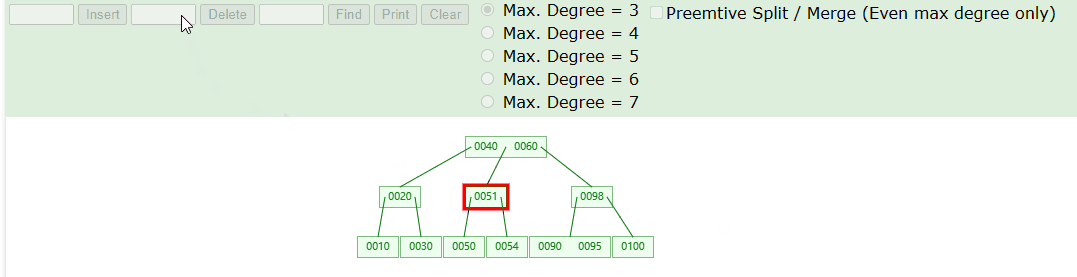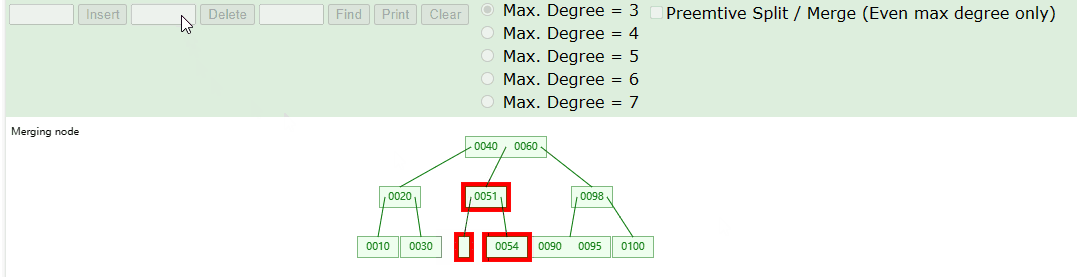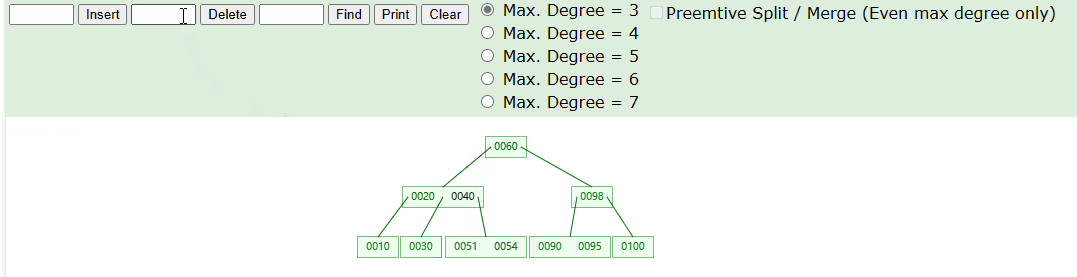
实现思路:
- Step-1:首先,我们需要检查相邻的节点。如果兄弟节点中有一个节点包含超过最小限制的元素数量,可以考虑从兄弟节点借一个元素来避免下溢。
- Step-2:然后,我们进行节点合并。如果相邻节点的元素数量都低于最小限制,那么考虑将这些节点合并。
- Step-3:最后,我们重复以上操作。如果在进行上述操作后,父节点也发生了下溢,可能需要递归地进行合并操作,以保持B树的平衡性。
5. 参考博文
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Wickson Blog!
评论






