数据结构-映射

1. 内容大纲

本章节代码：https://github.com/wicksonZhang/data-structure/tree/main/10-Map

---

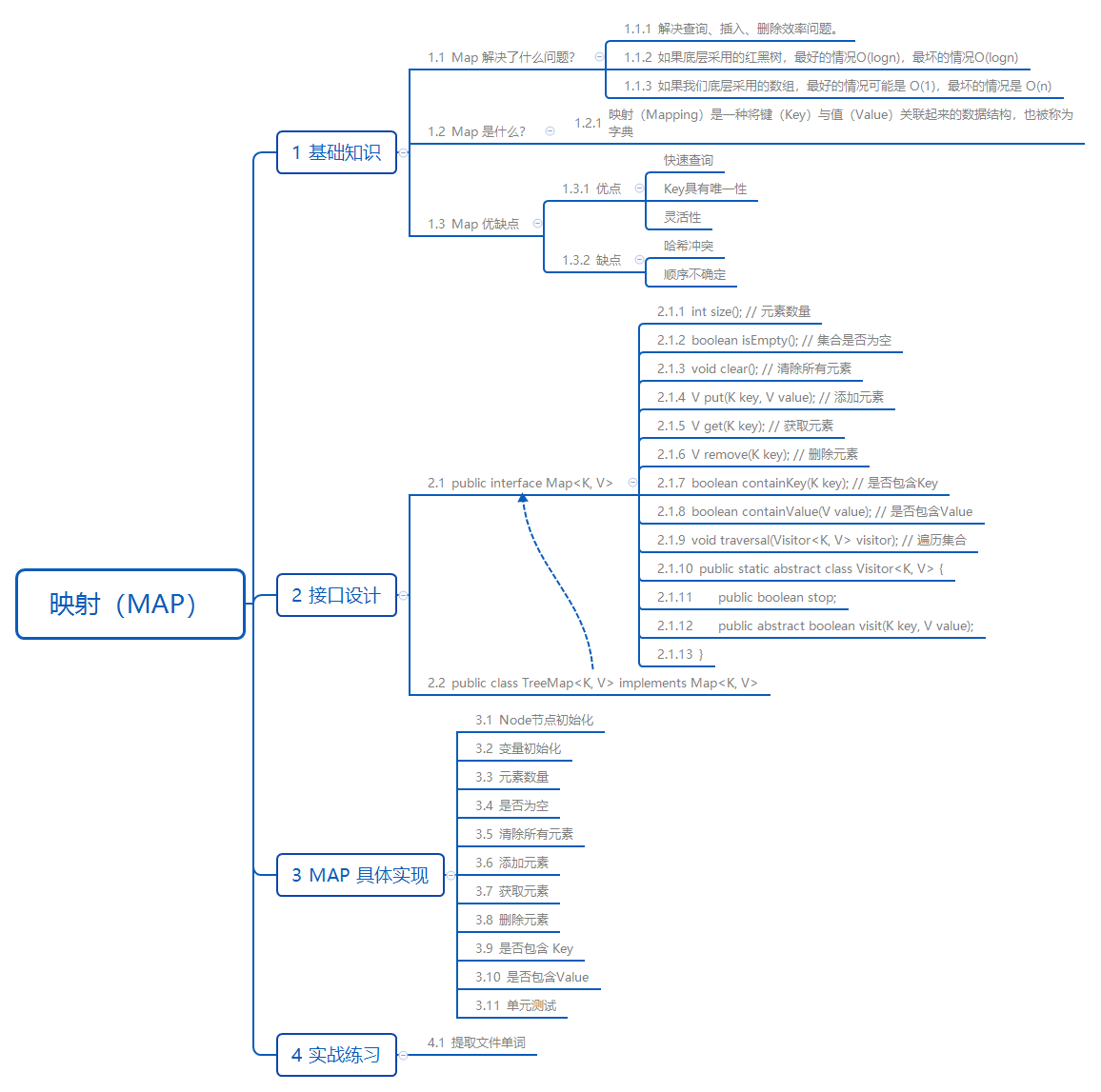
2. 基础知识

2.1. Map 解决了什么问题？

例如，我们在全国的行政区划表中，需要通过 行政区划 Code 找到对应的 Name 名称 , 如果使用的是数组进行存储的话，我们需要找到某个元素，可能是从头找到尾，时间复杂度可能为O(n)，这会导致效率会特别低。

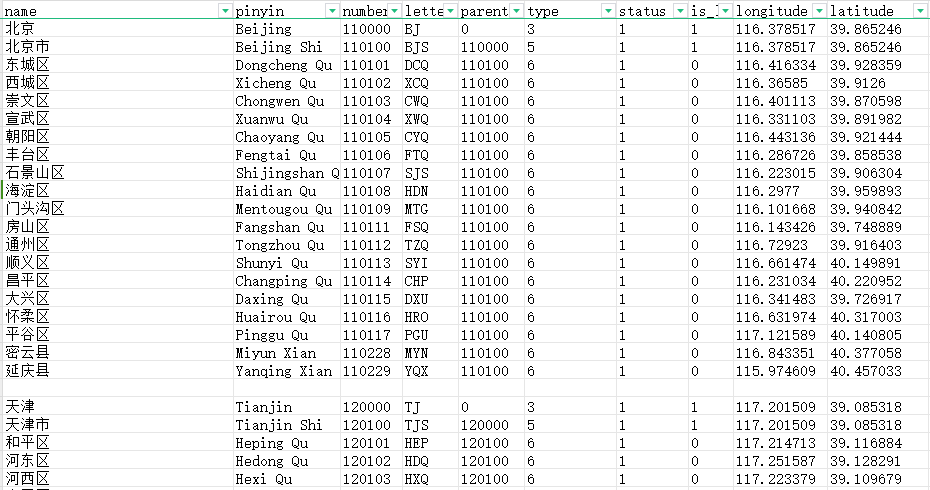
如果使用数组实现代码如下

• 如果我们底层采用的数组，最好的情况可能是 O(1)，最坏的情况是 O(n)，平均时间复杂度为 O(n)

// 使用List存储地址信息
List<DivisionInfo> divisionInfos = new ArrayList<>();
divisionInfos.add(new DivisionInfo(110000 "北京"));
divisionInfos.add(new DivisionInfo(120000, "天津"));
divisionInfos.add(new DivisionInfo(130000, "河北省"));
String name = "";
divisionInfos.forEach(divisionInfo -> {
    if (11000 == divisionInfo.getNumberCode()) {
        name = divisionInfo.getName();
        break;
    }
});

如果使用映射Map实现的代码如下

• 如果我们底层采用的红黑树，最好的情况O(logn)，最坏的情况O(logn)

Map<Integer, DivisionInfo> map = new HashMap<>();
map.put(110000, new DivisionInfo(110000 "北京"));
map.put(120000, new DivisionInfo(120000, "天津"));
map.put(130000, new DivisionInfo(130000, "河北省"));
// 直接通过Map获取信息
DivisionInfo divisionInfo = map.get(110000);

2.2. Map 是什么？

在数据结构中，映射（Mapping）是一种将键（Key）与值（Value）关联起来的结构，也被称为字典、哈希表或关联数组，具体的实现方式有很多种。

2.3. Map 优缺点

优点

1. 快速查询： Map提供了通过键直接访问值的机制，因此在查找特定元素时具有很高的效率。在Hash情况下，查找操作的时间复杂度是常量级别（O(1)）。在红黑树的情况下，查找操作的时间复杂度是对数级别（O(logn)）
2. 唯一性： Map中的键必须是唯一的，这确保了每个键都对应一个唯一的值。这在需要建立唯一关联关系的场景下非常有用。
3. 灵活性： Map适用于各种数据关联问题，可以用于构建字典、缓存、配置表等多种应用。不同实现方式（如哈希表、红黑树）可以满足不同的需求。

缺点

1. 哈希冲突： 在使用哈希表实现的Map中，可能会发生哈希冲突，即不同的键映射到相同的哈希桶。
2. 顺序不确定： Map通常不保证元素的顺序，这在一些情况下可能是一个缺点。
3. 复杂性： 某些Map的实现（例如红黑树）相对复杂，可能需要更多的计算资源和时间来维护数据结构的平衡性。

---

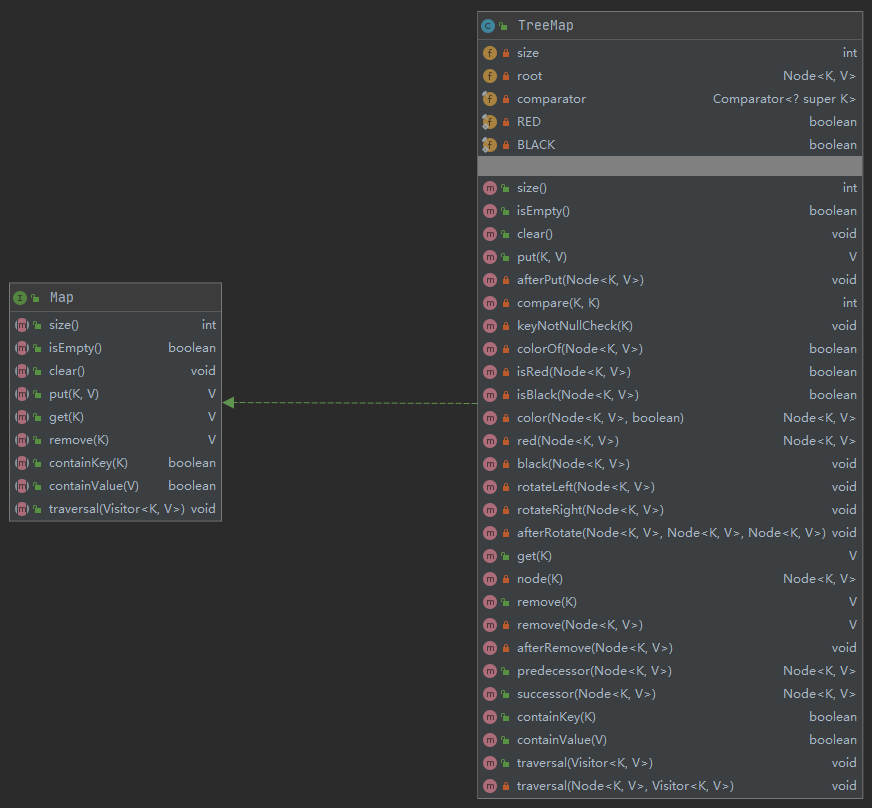
3. Map 接口设计

• Map<K,V>

public interface Map<K, V> {

    int size(); // 元素数量

    boolean isEmpty(); // 集合是否为空

    void clear(); // 清除所有元素

    V put(K key, V value); // 添加元素

    V get(K key); // 获取元素

    V remove(K key); // 删除元素

    boolean containKey(K key); // 是否包含Key

    boolean containValue(V value); // 是否包含Value

    void traversal(Visitor<K, V> visitor); // 遍历集合

    public static abstract class Visitor<K, V> {
        public boolean stop;

        public abstract boolean visit(K key, V value);
    }

}

---

4. Map 代码实现

4.1. Node节点初始化

/**
 * 基于红黑树实现映射
 *
 * @param <K>
 * @param <V>
 */
public class TreeMap<K, V> implements Map<K, V> {
    
    // TODO
    
	// 节点为红色
    private static final boolean RED = false;

    // 节点为黑色
    private static final boolean BLACK = true;

    /**
     * Node<K, V> 节点实现
     *
     * @param <K> key
     * @param <V> value
     */
    private static class Node<K, V> {
        // Key
        K key;

        // value
        V value;

        boolean color = RED;

        // 左子节点
        Node<K, V> leftNode;

        // 右子节点
        Node<K, V> rightNode;

        // 父级节点
        Node<K, V> parentNode;

        public Node(K key, V value, Node<K, V> parentNode) {
            this.key = key;
            this.value = value;
            this.parentNode = parentNode;
        }

        /**
         * 是否存在叶子节点
         *
         * @return boolean
         */
        public boolean isLeaf() {
            return leftNode == null && rightNode == null;
        }

        /**
         * 是否该节点的度为2
         *
         * @return boolean
         */
        public boolean hasTwoChildren() {
            return leftNode != null && rightNode != null;
        }

        /**
         * 是否是左子树
         *
         * @return boolean
         */
        public boolean isLeftChild() {
            return parentNode != null && this == parentNode.leftNode;
        }

        /**
         * 是否是右子树
         *
         * @return boolean
         */
        public boolean isRightChild() {
            return parentNode != null && this == parentNode.rightNode;
        }

        /**
         * 兄弟节点
         *
         * @return Node<E>
         */
        public Node<K, V> sibling() {
            if (isLeftChild()) {
                return parentNode.rightNode;
            }
            if (isRightChild()) {
                return parentNode.leftNode;
            }
            return null;
        }

    }

}

4.2. 变量初始化

public class TreeMap<K, V> implements Map<K, V> {

    /**
     * 节点数量
     */
    private int size;

    /**
     * 根节点
     */
    protected Node<K, V> root;

    /**
     * 比较器
     */
    private final Comparator<? super K> comparator;

    public TreeMap() {
        this(null);
    }

    public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }
    
}

4.3. 元素数量

/**
 * 元素数量 
 * @return int
 */
@Override
public int size() {
    return size;
}

4.4. 是否为空

/**
 * 是否为空
 *
 * @return boolean
 */
@Override
public boolean isEmpty() {
    return size == 0;
}

4.5. 清除所有元素

/**
 * 清除所有元素
 */
@Override
public void clear() {
    size = 0;
    root = null;
}

4.6. 添加元素

• 添加元素主要是基于红黑树，所以如下代码会涉及到相关红黑树代码

/**
 * 添加元素
 *
 * @param key   key
 * @param value value
 * @return V
 */
@Override
public V put(K key, V value) {
    keyNotNullCheck(key);

    // 添加第一个节点
    if (root == null) {
        root = new Node<>(key, value, null);
        size++;
        // 添加新节点之后进行处理
        afterPut(root);
        return null;
    }

    // Step2：如果当前节点不是父级节点，那就需要找到父级节点
    Node<K, V> node = root;
    Node<K, V> parent = root;
    int cmp = 0;
    // 将传递进来的元素与父级节点进行比较
    while (node != null) {
        cmp = compare(key, node.key);
        parent = node;
        if (cmp > 0) {
            node = node.rightNode;
        } else if (cmp < 0) {
            node = node.leftNode;
        } else {
            node.key = key;
            V oldValue = node.value;
            node.value = value;
            return oldValue;
        }
    }

    // Step3：我们将需要添加的元素添加在父级节点的那个位置
    Node<K, V> newNode = new Node<>(key, value, parent);
    if (cmp > 0) {
        parent.rightNode = newNode;
    } else {
        parent.leftNode = newNode;
    }
    size++;
    afterPut(newNode);
    return null;
}

/**
 * Map 添加元素之后作的处理
 *
 * @param node 节点
 */
private void afterPut(Node<K, V> node) {
    // 判断当前添加的父级节点
    Node<K, V> parentNode = node.parentNode;
    if (parentNode == null) {
        black(node);
        return;
    }

    /* Step-1：添加的节点父节点正好是 black */
    if (isBlack(parentNode)) {
        return;
    }

    /* Step-2：添加的节点 `uncle` 节点是 `Red` */
    // 叔父节点
    Node<K, V> uncle = parentNode.sibling();
    // 祖父节点
    Node<K, V> grandNode = red(parentNode.parentNode);
    if (isRed(uncle)) {
        // 将 parent 节点染成黑色
        black(parentNode);
        // 将 uncle 节点染成黑色
        black(uncle);
        // 将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。
        afterPut(grandNode);
        return;
    }

    /* Step-3：添加的节点 `uncle` 节点是 `Black` */
    // 判断父级节点是否是左子节点
    if (parentNode.isLeftChild()) { // L
        // 判断自己是否是左子节点
        if (node.isLeftChild()) { // LL
            // 将 `parent` 节点染成黑色
            black(parentNode);
        } else { // LR
            // 将 `parent` 节点染成黑色
            black(node);
            // 将 `parent` 进行左旋转，将二叉树变为 `LL`
            rotateLeft(parentNode);
        }
        // 将 `grand` 节点进行右旋
        rotateRight(grandNode);
    } else { // R
        if (node.isLeftChild()) { // RL
            // 将 `node` 节点染成黑色
            black(node);
            // 将 `parent` 进行右旋转，将二叉树变为 `RR`
            rotateRight(parentNode);
        } else { // RR
            // 将 `parent` 节点染成黑色
            black(parentNode);
        }
        // 将 `grand` 进行左旋转，使二叉树变得平衡
        rotateLeft(grandNode);
    }
}

4.7. 获取元素

/**
 * 获取元素
 *
 * @param key Key
 * @return V
 */
@Override
public V get(K key) {
    Node<K, V> node = node(key);
    return node != null ? node.value : null;
}

/**
 * 获取元素的节点
 *
 * @param key Key
 * @return Node<K, V>
 */
private Node<K, V> node(K key) {
    if (key == null) {
        return null;
    }
    Node<K, V> node = this.root;
    while (node != null) {
        int compare = compare(key, node.key);
        if (compare > 0) {
            node = node.rightNode;
        } else if (compare < 0) {
            node = node.leftNode;
        } else {
            return node;
        }
    }
    return null;
}

4.8. 删除元素

/**
 * 删除元素
 *
 * @param key key
 * @return V
 */
@Override
public V remove(K key) {
    return remove(node(key));
}

/**
 * 删除节点
 *
 * @param node 节点
 * @return V
 */
private V remove(Node<K, V> node) {
    if (node == null) {
        return null;
    }
    V oldValue = node.value;
    // 删除度为 2 的节点
    if (node.hasTwoChildren()) {
        // 找到当前元素的前驱节点
        Node<K, V> predecessorNode = predecessor(node);
        node.key = predecessorNode.key;
        node.value = predecessorNode.value;
        node = predecessorNode;
    }

    // 删除 node：node节点的度要么是1，要么是0
    Node<K, V> removeNode = node.leftNode != null ? node.leftNode : node.rightNode;

    // 如果 node 是为删除度为1的节点
    if (removeNode != null) {
        // 更换父级节点
        removeNode.parentNode = node.parentNode;
        if (removeNode.parentNode == null) { // 当只存在根节点，根节点的度为1的情况
            root = removeNode;
        } else if (node == node.parentNode.leftNode) {
            node.parentNode.leftNode = removeNode;
        } else {
            node.parentNode.rightNode = removeNode;
        }
        // 删除之后的处理
        afterRemove(removeNode);
    } else if (node.parentNode == null) { // 删除叶子节点, 且只有根节点元素
        root = null;
        // 删除之后的处理
        afterRemove(node);
    } else { // 删除叶子节点, 有可能当前节点在父级节点的左边，也有可能在父级节点的右边
        if (node == node.parentNode.leftNode) {
            node.parentNode.leftNode = null;
        } else {
            node.parentNode.rightNode = null;
        }
        // 删除之后的处理
        afterRemove(node);
    }
    size--;
    return oldValue;
}

4.9. 是否包含 Key

/**
 * 是否包含Key
 *
 * @param key key
 * @return boolean
 */
@Override
public boolean containKey(K key) {
    return node(key) != null;
}

4.10. 是否包含Value

/**
 * 是否包含 Value
 *
 * @param value value
 * @return boolean
 */
@Override
public boolean containValue(V value) {
    // 通过队列实现
    Queue<Node<K, V>> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        Node<K, V> node = queue.poll();
        if (Objects.equals(value, node.value)) return true;
        if (node.leftNode != null) {
            queue.offer(node.leftNode);
        }
        if (node.rightNode != null) {
            queue.offer(node.rightNode);
        }
    }
    return false;
}

4.11. 单元测试

public class TreeMapTest {

    private TreeMap<Integer, String> treeMap;

    @BeforeEach
    public void setUp() {
        // 在每个测试方法执行之前初始化 TreeMap
        treeMap = new TreeMap<>();
        treeMap.put(5, "five");
        treeMap.put(3, "three");
        treeMap.put(8, "eight");
        treeMap.put(2, "two");
        treeMap.put(4, "four");
    }

    @Test
    public void testSize() {
        Assertions.assertEquals(5, treeMap.size());
    }

    @Test
    public void testIsEmpty() {
        Assertions.assertFalse(treeMap.isEmpty());
    }

    @Test
    public void testClear() {
        treeMap.clear();
        Assertions.assertEquals(0, treeMap.size());
        Assertions.assertTrue(treeMap.isEmpty());
    }

    @Test
    public void testPut() {
        // 添加新元素
        Assertions.assertNull(treeMap.put(1, "one"));
        Assertions.assertEquals(6, treeMap.size());

        // 更新已存在的元素
        Assertions.assertEquals("one", treeMap.put(1, "newOne"));
        Assertions.assertEquals(6, treeMap.size());
    }

    @Test
    public void testGet() {
        Assertions.assertEquals("five", treeMap.get(5));
        Assertions.assertEquals("three", treeMap.get(3));
        Assertions.assertNull(treeMap.get(10)); // 不存在的键返回 null
    }

    @Test
    public void testRemove() {
        Assertions.assertEquals("five", treeMap.remove(5));
        Assertions.assertNull(treeMap.get(5)); // 已删除的键应返回 null
        Assertions.assertEquals(4, treeMap.size());
    }

    @Test
    public void testContainKey() {
        Assertions.assertTrue(treeMap.containKey(3));
        Assertions.assertFalse(treeMap.containKey(10));
    }

    @Test
    public void testContainValue() {
        Assertions.assertTrue(treeMap.containValue("eight"));
        Assertions.assertFalse(treeMap.containValue("ten"));
    }

    @Test
    public void testTraversal() {
        // 创建 Visitor 接口的实现类，用于测试遍历
        class TestVisitor extends Map.Visitor<Integer, String> {
            final StringBuilder result = new StringBuilder();
            @Override
            public boolean visit(Integer key, String value) {
                result.append(key).append(":").append(value).append(" ");
                return false; // 返回 false，以便遍历所有节点
            }
        }

        TestVisitor visitor = new TestVisitor();
        treeMap.traversal(visitor);

        Assertions.assertEquals("2:two 3:three 4:four 5:five 8:eight ", visitor.result.toString());
    }
}

---

5. 实战练习

5.1. 文件打印

/**
 * 性能对比：红黑树和链表
 */
public class ComparisonTest {

    @Test
    public void treeMapTest() {
        Times.test("treeMapTest", () -> common(new TreeMap<>(), file()));
    }

    public String[] file() {
        FileInfo fileInfo = Files.read("D:\\java\\jdk-8\\jdk1.8.0_211\\src\\java\\util",
                new String[]{"java"});

        System.out.println("文件数量：" + fileInfo.getFiles());
        System.out.println("代码行数：" + fileInfo.getLines());
        String[] words = fileInfo.words();
        System.out.println("单词数量：" + words.length);
        return words;
    }

    public void common(TreeMap<String, Integer> treeMap, String[] words) {
        // 添加
        for (String word : words) {
            Integer count = treeMap.get(word);
            Integer totalCount = count == null ? 1 : count + 1;
            treeMap.put(word, totalCount);
        }
        // 创建 Visitor 接口的实现类，用于测试遍历
        treeMap.traversal(new Map.Visitor<String, Integer>() {
            @Override
            public boolean visit(String key, Integer value) {
               // System.out.println("key = " + key + ", " + "value = " + value);
                return false;
            }
        });
        // 查询
        for (String word : words) {
            treeMap.containKey(word);
        }
        // 删除
        for (String word : words) {
            treeMap.remove(word);
        }
    }

}

• 结果信息

【treeMapTest】
开始：20:13:29.446
文件数量：364
代码行数：212580
单词数量：879293
结束：20:13:30.896
耗时：1.45秒

---

6. 参考博文

• 恋上数据结构与算法(第一季)-MJ大神精选