数据结构-哈夫曼树
1. 哈夫曼树主要解决了什么问题?
哈夫曼树(Huffman Tree):主要解决了数据压缩中的编码问题。在数据传输和存储中,经常需要对数据进行压缩以减少所需的存储空间或传输带宽。
例如,我们需要将字符串【ABBBCCCCCCCCDDDDDDEE】转为二进制编码进行传输,需要进行如下操作:
- 首先,将字母转为 ASCII 编码,也就是 A-65、B-66、C-67 等等。
- 然后,我们再将对应的 ASCII 编码转为二进制,也就是 A-65-1000001、B-66-1000010 等等。
- 最后,将所有的字符串进行上述操作,得出的二进制字符串的长度为 160 位。
如果像上诉这个操作一定会导致我们出现大量的二进制位,占用大量的存储空间。这时我们就可以通过 哈夫曼编码 就可以解决这个问题了。
2. 哈夫曼树是什么?
哈夫曼树(Huffman Tree)是一种特殊的二叉树,用于构建哈夫曼编码,主要用于数据压缩中。
- 如果我们需要构建 “this is an example of a huffman tree” 使用哈夫曼树可能就是像下图展示这样。
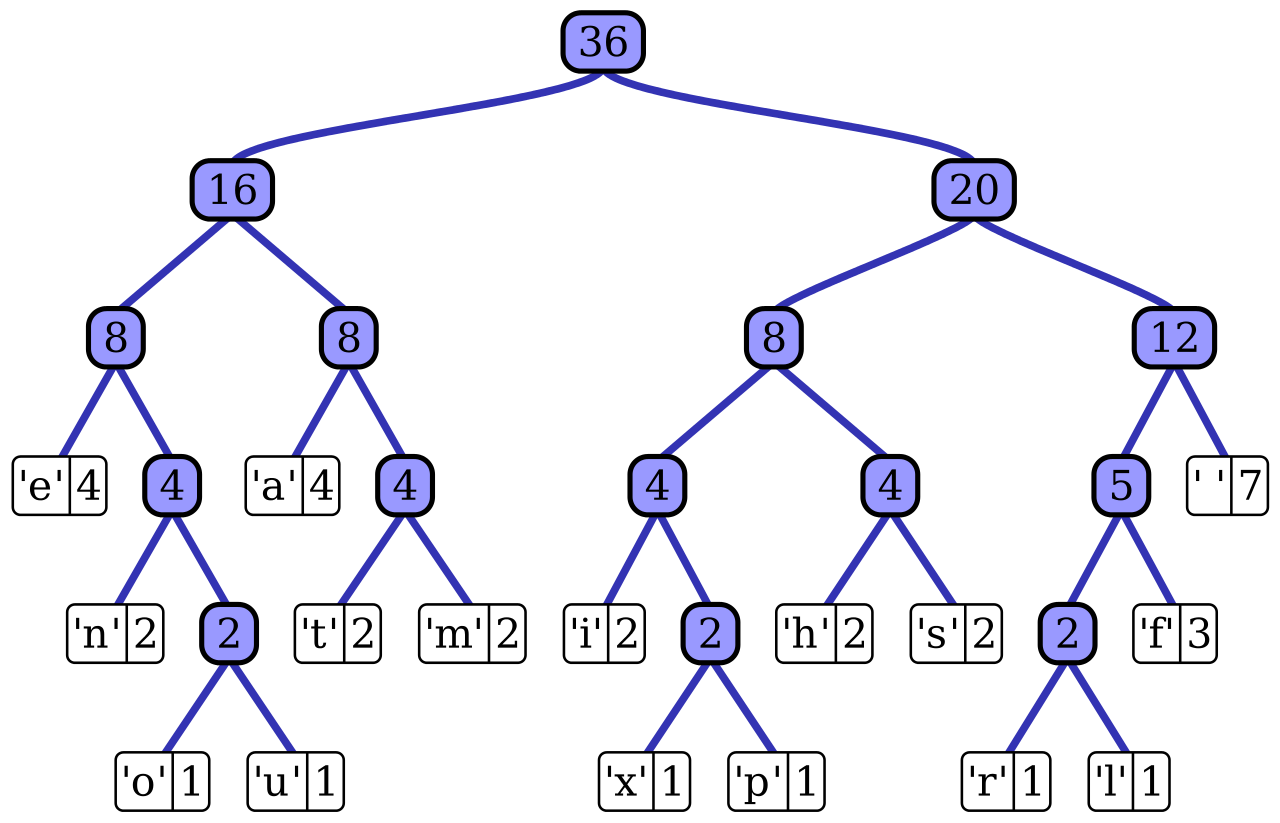
3. 如何构建一颗哈夫曼树
我们以开头的字符串 【
ABBBCCCCCCCCDDDDDDEE】为例。
实现步骤
1 | Step-1:计算出每个字符出现的权值(权重,就是出现的次数) |
计算出每个字符出现的权值(权重,就是出现的次数)
| A | B | C | D | E |
|---|---|---|---|---|
| 1 | 3 | 8 | 6 | 2 |
以权值作为根节点构建 n 棵二叉树,组成森林

在森林中选出 2 个根节点最小的树合并,作为一棵新树的左右子树,且新树的根节点为其左右子树根节点之和
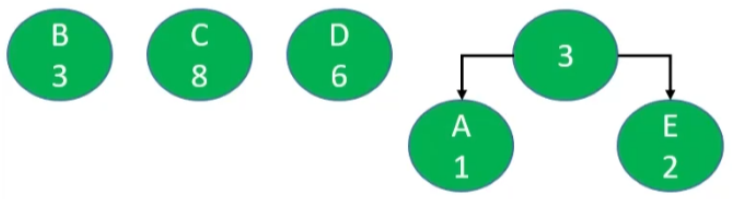
- 首先,作为权重最小的两个根节点是 A、E ,作为左右子节点,根节点就是左右子节点的和。再从森林中删除 A、E 节点
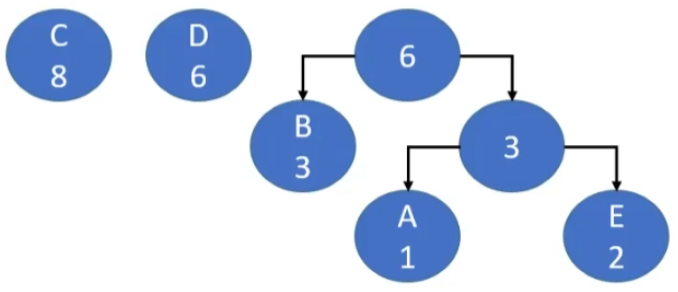
- 接着,作为权重最小的根节点就是 B,作为左子节点,根节点就是 (A、E 根节点) + (B 节点)的和。再从森林中删除 B 节点
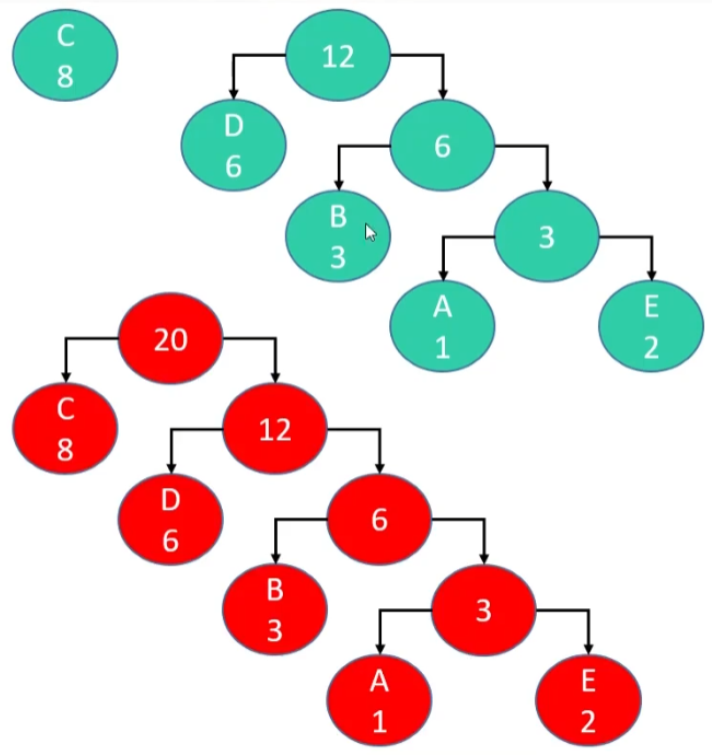
- 重复上诉操作
重复 3、4 步骤,直到森林只剩一棵树为止,该树即为哈夫曼树
4. 如何计算哈夫曼编码
通过上面构建的哈夫曼树,我们已 左子节点 作为 left(0),右子节点 作为 right(1),可以得出如下对应的哈夫曼编码。
- 例如,A从根节点从右到左分别是12、6、3、A,即 1110
| A | B | C | D | E |
|---|---|---|---|---|
| 1110 | 110 | 0 | 10 | 1111 |
【ABBBCCCCCCCCDDDDDDEE】哈夫曼编码每个字符对应的结果是:1110 110 110 110 0 0 0 0 0 0 0 0 10 10 10 10 10 10 1111
5. 总结
- n 个权值构建出来的哈夫曼树拥有 n 个叶子节点。
- 每个哈夫曼编码都不是另一个哈夫曼编码的前缀。
- 哈夫曼树是带权路径长度最短的树,权值较大的节点离根节点较近。
- 带权路径长度:树中所有的叶子节点的权值乘上其到根节点的路径长度与最终的哈夫曼编码总长度成正比关系。
6. 参考博文
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Wickson Blog!
评论






