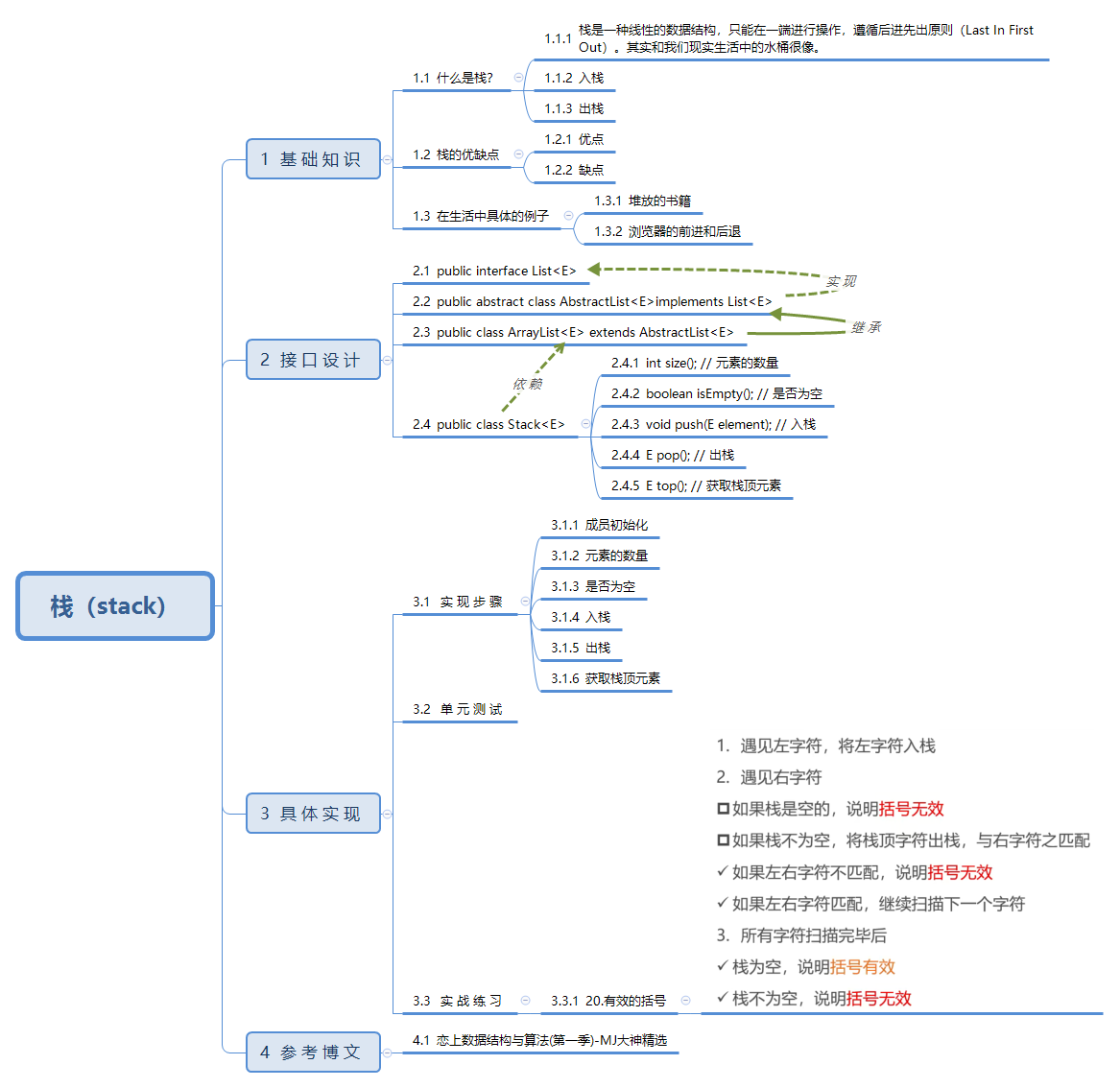
1. 内容大纲
本章节的代码:https://github.com/wicksonZhang/data-structure/tree/main/3-Stack
2. 基础知识
2.1. 什么是栈?
栈是一种线性的数据结构,只能在一端进行操作,遵循后进先出原则(Last In First Out)。其实和我们现实生活中的水桶很像。
2.2. 栈的优缺点
优点
- 简单易用: 栈的操作简单明了,主要包括入栈(push)和出栈(pop),易于实现和理解。
- 快速操作: 入栈和出栈操作在时间复杂度上通常为常数时间,因此执行速度很快。
- 内存管理: 在计算机科学中,栈用于函数调用和参数传递。
缺点
- 大小限制: 栈的大小通常是固定的,取决于操作系统或编程语言的限制。
- 数据访问限制: 栈的特性决定了只能访问最顶部的元素,无法直接访问其他位置的元素。
- 不灵活: 由于其后进先出的特性,有时并不适合某些特定的问题解决方案。
2.3. 在生活中具体的例子
- 盘子堆叠: 像洗碗时将碗堆叠起来,最先进来的最后出现。
- 书籍叠放: 将书籍垒成一摞,最后放上去的会最先被取走。
- 浏览器的前进和后退
3. 接口设计
关于 List<E>、AbstractList<E> 、ArrayList<E> 具体可参考《数据结构-动态数组》
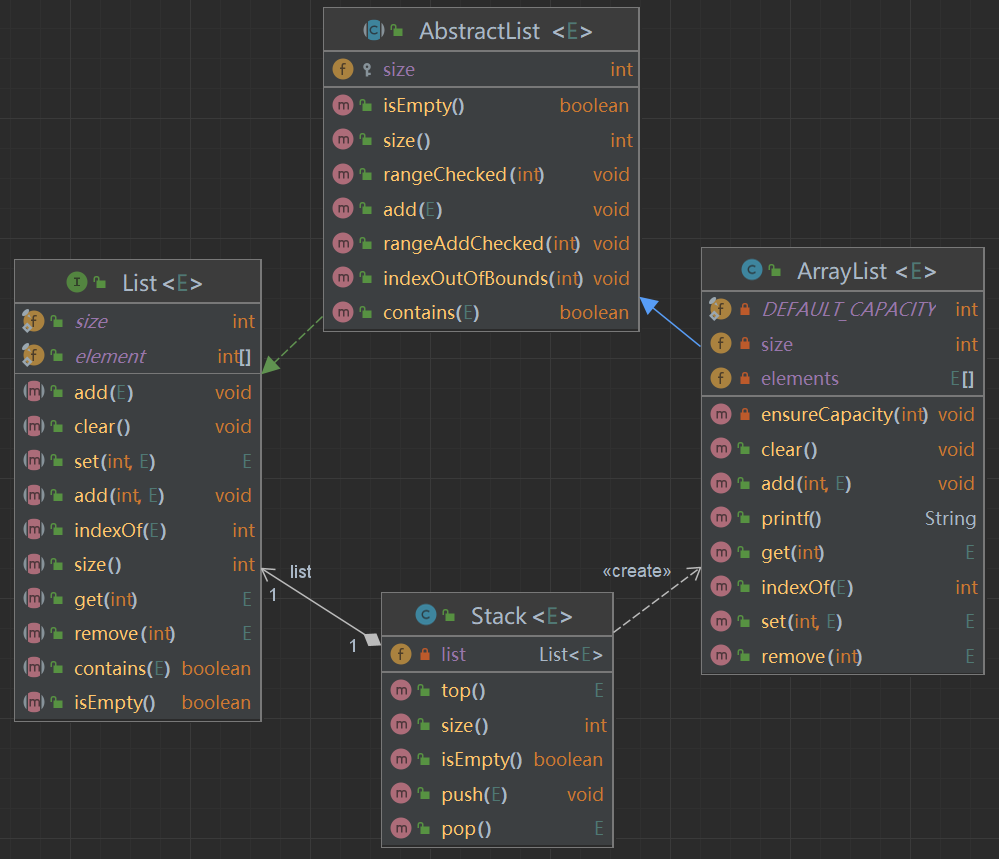
我们栈也是线性结构,与数组的区别就是栈存在一个栈底,所以我们可以基于动态数组的方式构建栈。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public class Stack<E> {
public int size() {}
public boolean isEmpty() {}
public void push(E element) {}
public E pop() { }
public E top() {}
}
|
4. 代码实现
4.1. 成员初始化
1
2
3
4
5
| public class Stack<E> {
private List<E> list = new ArrayList<>();
}
|
4.2. 元素的数量
1
2
3
4
5
6
7
8
|
public int size() {
return list.size();
}
|
4.3. 是否为空
1
2
3
4
5
6
7
8
|
public boolean isEmpty() {
return list.isEmpty();
}
|
4.4. 入栈
入栈:本质就是将元素有序的添加到动态数组中。

1
2
3
4
5
6
7
8
|
public void push(E element) {
list.add(element);
}
|
4.5. 出栈
出栈:我们只需要移除数组中的最后一个元素。

1
2
3
4
5
6
7
8
|
public E pop() {
return list.remove(size() - 1);
}
|
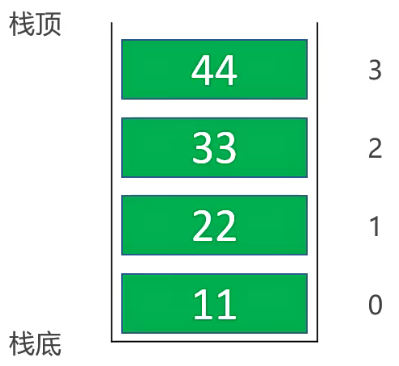
4.6. 获取栈顶元素
获取栈顶元素:就是获取动态数组中的最后一个元素。
1
2
3
4
5
6
7
8
|
public E top() {
return list.get(size() - 1);
}
|
4.7. 测试用例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public class StackTest {
@Test
public void testEmptyStack() {
Stack<Integer> stack = new Stack<>();
assertTrue(stack.isEmpty());
assertEquals(0, stack.size());
}
@Test
public void testPushAndPop() {
Stack<String> stack = new Stack<>();
assertTrue(stack.isEmpty());
stack.push("First");
stack.push("Second");
assertFalse(stack.isEmpty());
assertEquals(2, stack.size());
assertEquals("Second", stack.pop());
assertEquals("First", stack.pop());
assertTrue(stack.isEmpty());
assertEquals(0, stack.size());
}
@Test
public void testTop() {
Stack<Double> stack = new Stack<>();
stack.push(3.14);
assertEquals(3.14, stack.top());
assertEquals(1, stack.size());
}
@Test
public void testPopOnEmptyStack() {
Stack<Character> stack = new Stack<>();
assertThrows(IndexOutOfBoundsException.class, stack::pop);
}
@Test
public void testTopOnEmptyStack() {
Stack<Boolean> stack = new Stack<>();
assertThrows(IndexOutOfBoundsException.class, stack::top);
}
}
|
5. 实战练习
5.1. 有效的括号
地址:https://leetcode.cn/problems/valid-parentheses/description/
需求

实现思路
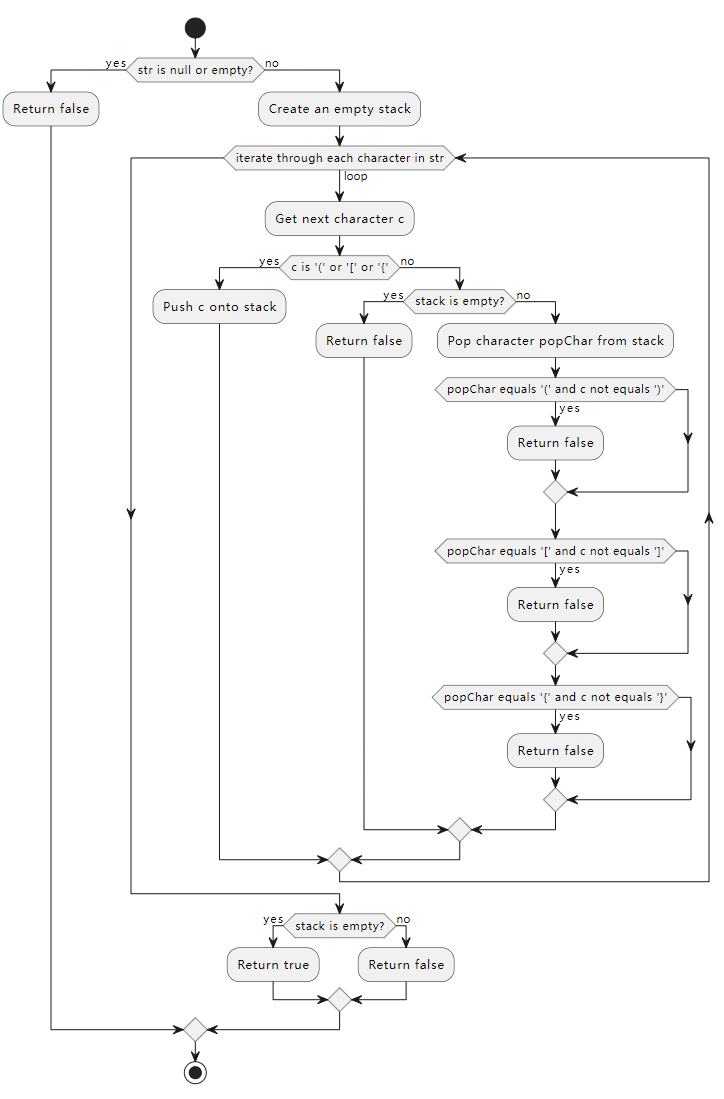
- 遇见左字符,将左字符入栈
- 遇见右字符
- 如果栈是空的,说明括号无效
- 如果栈不为空,将栈顶字符出栈,与右字符之匹配
- 如果左右字符不匹配,说明括号无效
- 如果左右字符匹配,继续扫描下一个字符
- 所有字符扫描完毕后
UML 流程图
具体代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public static boolean isValid(String str) {
if (str == null || "".equals(str)) {
return false;
}
Stack<Character> stack = new Stack<>();
for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
} else {
if (stack.isEmpty()) return false;
char popChar = stack.pop();
if (popChar == '(' && c != ')') return false;
if (popChar == '[' && c != ']') return false;
if (popChar == '{' && c != '}') return false;
}
}
return stack.isEmpty();
}
|
6. 参考博文













