1. 内容大纲

二叉树

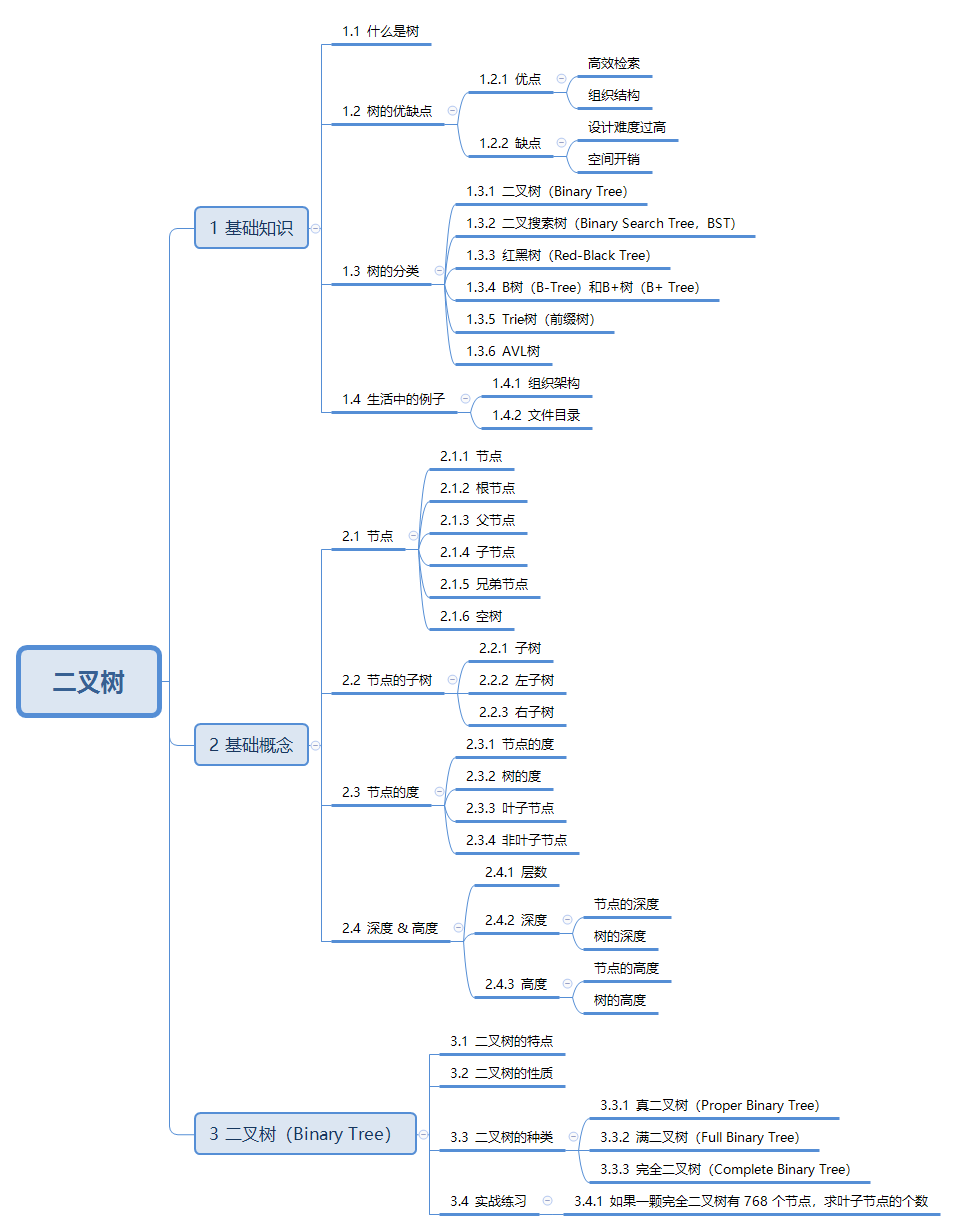
2. 基础知识

2.1. 什么是树

树：一种树形的数据结构，主要由节点组成（Node），这些节点以层次关系连接。树的结构类似于自然界中的树。

image-20231129095828884

2.2. 树的优缺点

优点

  1. 高效的数据检索：树结构允许快速的搜索、插入和删除操作。对于平衡树（如平衡二叉树、红黑树等），这些操作的时间复杂度可以达到对数级别。
  2. 组织结构：树形结构能够自然地组织和表示层次关系的数据，例如文件系统中的目录结构。

缺点

  1. 空间开销：树结构可能会占用较多的额外空间来存储节点之间的连接关系，特别是在树的节点数量较多时。
  2. 设计难度：选择合适的树结构并对其进行有效的实现可能需要一定的技术和理解，尤其是对于复杂的树结构。

2.3. 树的分类

  1. 二叉树（Binary Tree）

    • 特点：每个节点最多有两个子节点。

    • 应用场景：在计算机科学中广泛应用，例如在编程语言中的表达式解析、排序算法中的二叉搜索树（BST）、哈夫曼树（用于数据压缩）

  2. 二叉搜索树（Binary Search Tree，BST）

    • 特点：是一种有序的二叉树，左子树的节点值小于父节点，右子树的节点值大于父节点。

    • 应用场景：常用于实现动态集合的数据结构，例如在数据库中的索引结构、实现字典或映射等。

  3. 红黑树（Red-Black Tree）

    • 特点：一种自平衡的二叉搜索树，通过维护节点的颜色和一些规则来确保树的平衡性。

    • 应用场景：被广泛用于实现集合、映射等数据结构，Java中 HashMap 的底层就是采用的红黑树

  4. B树（B-Tree）和 B+树（B+ Tree）

    • 特点：多路搜索树，每个节点可以拥有多个子节点，用于磁盘和数据库等存储系统。

    • 应用场景：常用于数据库索引、文件系统中的文件组织、存储大量数据的数据结构。

  5. Trie 树（前缀树）

    • 特点：用于存储关联数组，其中键通常是字符串，利用键的前缀来构建树结构。

    • 应用场景：常用于搜索引擎中的单词自动补全、字典等需要快速查找的场景。

  6. AVL 树

    • 特点：一种自平衡二叉搜索树，通过旋转操作来维护平衡。

    • 应用场景：常用于需要严格保证平衡性的场景，例如实时系统、数据库索引等。

2.4. 生活中对应的场景

  • 组织架构

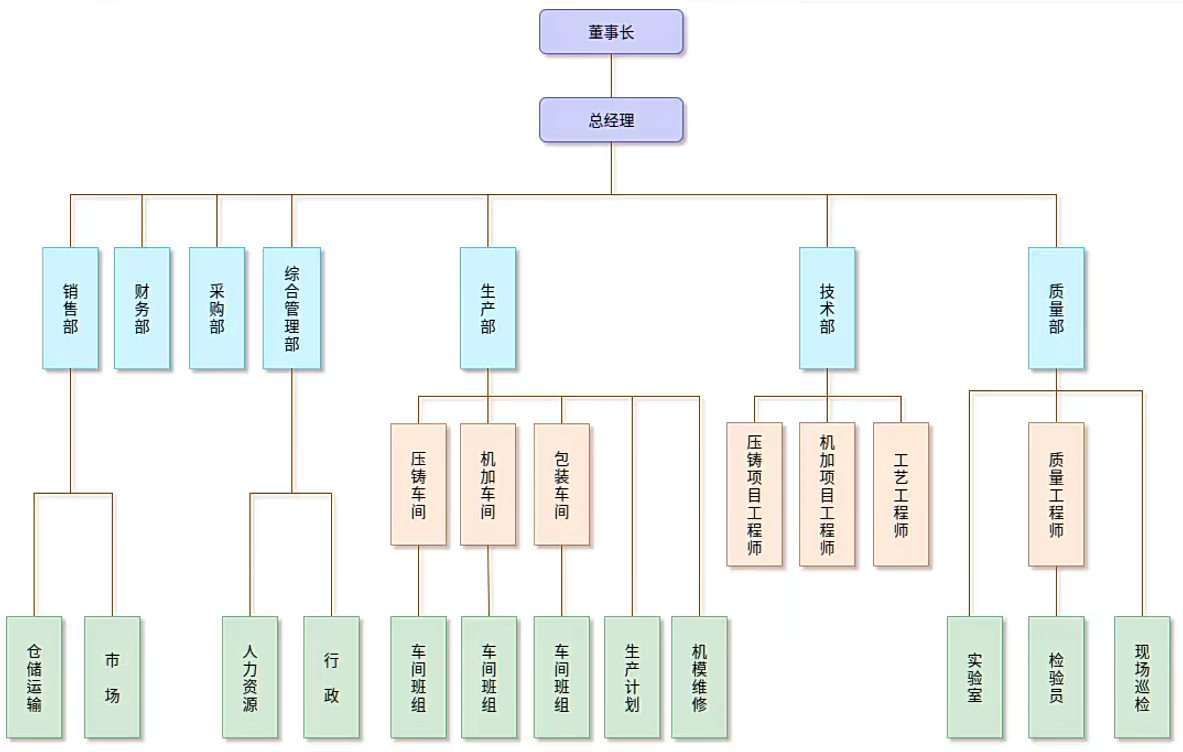
    image-20231128230254168

  • 文件目录

    image-20240310220611199

3. 基础概念

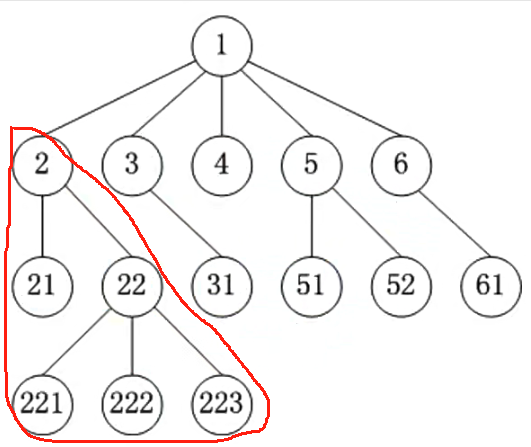
下图是一个二叉树的基本信息，我们如下标题的 节点、节点的子树、节点的度、深度&高度 中的例子都是以下图为主。

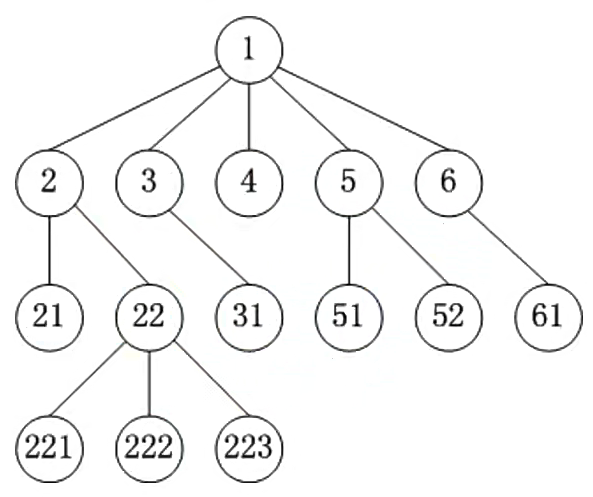
image-20231128230632249

3.1. 节点

节点：树的基本单元，可以包含数据或元素。

  • 例如：1，2，3，4，5，6，21. . .

3.1.1. 根节点

根节点：树的顶部节点，是树的起点。

  • 例如：1

3.1.2. 父节点

父节点：子节点的连接点。

  • 例如：1，2，3，5，6，22 . . .

3.1.3. 子节点

子节点：子节点是父节点的直接下属。

  • 例如：2，3，4，5，6 就是 1 的子节点

3.1.4. 兄弟节点

兄弟节点：兄弟节点是同一个父节点的子节点。

  • 例如，2，3，4，5，6 就是兄弟节点，但 21，31 就不是兄弟节点。

3.1.5. 空树

空树：指的是一棵树可以没有任何节点

3.2. 节点的子树

3.2.1. 子树

子树：指根节点中子节点产生的树。

  • 例如：2，21，22，221，222，223

3.2.2. 左子树

左子树：指当前节点左侧的树。

  • 例如：2 的左子树就是21

image-20231128231547856

3.2.3. 右子树

右子树：指子节点右侧的树。

  • 例如：2的右子树就是22

3.3. 节点的度

节点的度：子树的个数。

  • 例如：根节点1的度就是5（2，3，4，5，6）

3.3.1. 树的度

树的度：所有节点度中的最大值。

  • 例如：根节点1最大也就是5

3.3.2. 叶子节点

叶子节点：度为 0 的节点。

  • 例如：21，221，222，223，4，51，52，61

3.3.3. 非叶子节点

非叶子节点：度非 0 的节点。

  • 例如 2，3，5，6

3.4. 深度 && 高度

3.4.1. 层数

层数：根节点（1）为第 1 层，子节点（2，3，4，5，6）为第 2 层，然后以此类推。

3.4.2. 深度

节点的深度

  • 从根节点到当前节点的唯一路径上的节点总数。
  • 例如，当前节点为 2 ，那么深度就是2（1，2），当前节点为 31 ，那么深度就是3（1，3，31）

树的深度

  • 所有节点深度中的最大值。
  • 例如，根节点 1 的深度为 4 （1，2，22，223）

3.4.3. 高度

节点的高度

  • 从当前节点到最远叶子节点的路径上的节点总数。
  • 例如，当前节点2的高度就是3（2，22，221）

树的高度

  • 所有节点高度中的最大值，树的深度等于树的高度。
  • 例如 根节点 1 的高度就是 4 （1，2，22，223）

4. 二叉树（Binary Tree）

4.1. 二叉树的特点

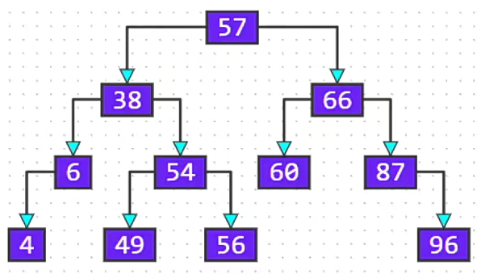
image-20231129135054480

  • 二叉树每个节点最多有两个子节点
  • 左子树和右子树必须保证顺序

4.2. 二叉树的特性

我们下图中的例子以如下图中的二叉树为准

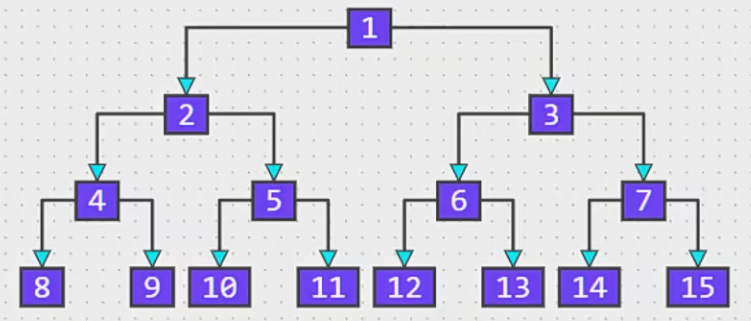
  1. 非空二叉树的第 i 层，最多有 2^(i-1) 个节点 （i >= 1）

    • 例如：第 4 层，2^(4 - 1) = 8

  2. 在高度为 h 的二叉树上最多有 2^h - 1 个节点（h >= 1）

    • 例如：高度为 4，2^4 - 1 = 15

  3. 对于任何一棵非空二叉树，如果叶子节点个数为 n0，度为2的节点个数为 n2，则有：n0 = n2+1。

    • n0 = 8（度为0的节点，例如：8，9，10，11，12，13，14，15）

    • n2 = 7（度为2的节点，例如：1，2，3，4，5，6，7）

    • n0 = n2 + 1

  4. n0 = n2 + 1，公式推导如下：

    • 假设节点总数为 n , 则 n = n0 + n1 + n2，即度为0，为1，为2 的总和。

      • n0 = 8（8，9，10，11，12，13，14，15）
      • n1 = 0（0）
      • n2 = 7（1，2，3，4，5，6，7）

    • 假设边数为 t，边数（节点的左右两根连接线）。

      • t = n1 + 2 * n2 = 14，即 n1 = 0（0）、n2 = 7（1，2，3，4，5，6，7）
      • t = n - 1 = 14，即 n = 15，由于根节点是没有边的，所有需要 - 1.
      • 其中 n 是可以换算为 n0 + n1 + n2 ，所以可以推导为 n1 + 2 * n2 = （n0 + n1 + n2） - 1
      • 则 n0 = n2 + 1

5. 二叉树的种类

5.1. 真二叉树（Proper Binary Tree）

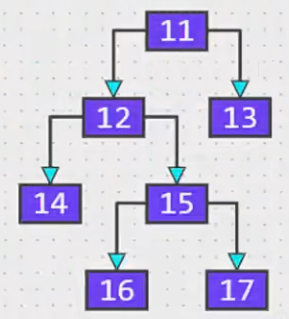
image-20231129150130016

5.1.1. 真二叉树特点

真二叉树：所有节点要么为 0 ，要么为 2

5.2. 满二叉树（Full Binary Tree）

image-20231129150629477

5.2.1. 满二叉树特点

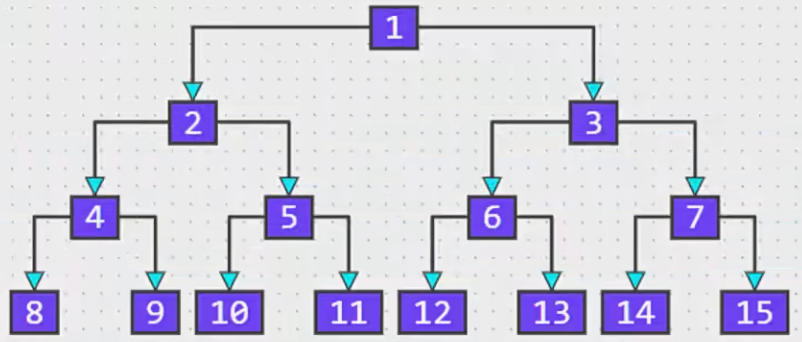
满二叉树：所有节点的度要么为 0 ，要么为 2。且所有的叶子节点都在最后一层。

注意：满二叉树一定是真二叉树，真二叉树不一定是满二叉树。

5.2.2. 满二叉树特性

  • 假设满二叉树的高度为 h (h >= 1)，则可以得到如下结论：
    • 第 i 层的节点数量：2^(i - 1)，例如，上图中第二层(2，3)的节点数量为 2^(2 - 1) = 2
    • 叶子节点数量：2^(h - 1)，例如，上图中高度为4的节点数量为 2^(4-1) = 8
    • 总的节点数量 n：
      • n = 2^h - 1 => (2^0 + 2^1 + 2^2 + … + 2^(h - 1))
      • h = log2(n + 1)

5.3. 完全二叉树（Complete Binary Tree）

image-20231129153901627

5.3.1. 完全二叉树特点

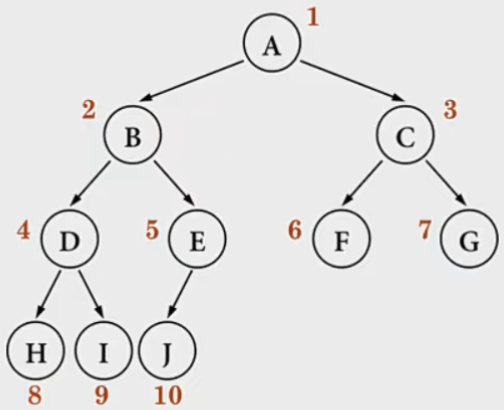
  1. 完全二叉树：叶子节点只会出现最后 2 层，且最后 1 层的叶子节点都靠左对齐。
  2. 可以理解为完全二叉树是从上到下，从左到右都是向左靠齐。
  3. 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树
  4. 度为 1 的节点只有左子树，子节点要么是 1 个，要么是 0 个。

5.3.2. 完全二叉树特性

  1. 假设完全二叉树的高度为 h（h >= 1），则可以得到如下结论：

    • 节点总数：至少有 2^(h - 1) 个节点，以上图为例，即（2^0 + 2^1 + 2^2 + … + 2^(h - 2) + 1）= 8
    • 节点总数：至多有 2^h - 1 个节点，即（2^0 + 2^1 + 2^2 + …… + 2^(h - 1)，满二叉树）= 15
    • 总节点数为n
      • 2^(h - 1) <= n < 2^h
      • h - 1 <= log2n < h
      • h = floor(log2n) + 1
      • floor 向下取整，ceiling 向上取整

  2. 假设一颗有 n 个节点的完全二叉树（n > 0）, 从上到下、从左到右对节点从 1 开始进行编号，则任意第 i 个节点可以得到如下结论：

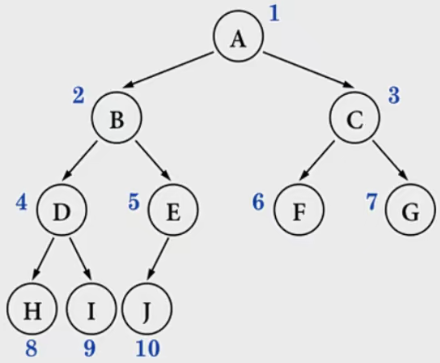
    image-20231129165032068

    • i = 1，它是根节点。以上图节点A为例, i = 1 就是根节点
    • i > 1，它的父节点编号为 floor(i / 2)。以上图节点G为例，floor(7 / 2) = 3
    • 2i <= n，它的左子节点编号为 2i。以上图节点E为例，2 * 5 = 10
    • 2i > n，它无左子节点。以上图节点F为例，2 * 6 > 10
    • 2i + 1 <= n，它的右子节点编号为 2i + 1。以上图节点D为例，2 * 4 + 1 = 9
    • 2i + 1 > n，它无右子节点。以上图节点E为例，2 * 5 + 1 > 10

  3. 假设一颗有 n 个节点的完全二叉树（n > 0）, 从上到下、从左到右对节点从 0 开始进行编号，则任意第 i 个节点可以得到如下结论：

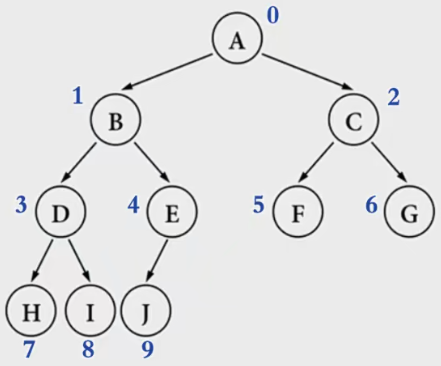
    image-20231129164411205

    • i = 0，它是根节点。以上图节点A为例, i = 0 就是根节点

    • i > 0，它的父节点编号为 floor((i - 1) / 2)。以上图节点G为例，floor((6 - 1) / 2) = 2

    • 2i + 1 <= n - 1，它的左子节点编号为 2i + 1。以上图节点E为例，2 * 4 + 1 = 9

    • 2i + 1 > n - 1，它无左子节点。以上图节点F为例，2 * 5 > 9 - 1

    • 2i + 1 <= n，它的右子节点编号为 2i + 1。以上图节点D为例，2 * 4 + 1 = 9

    • 2i + 1 <= n - 1, 它的右子节点编号为 2i + 2。以上图节点D为例，2 * 3 + 2 = 8

6. 实战练习

leetcode地址：https://leetcode-cn.com/problems/find-leaves-of-binary-tree/

需求

  • 如果一颗完全二叉树有 768 个节点，求叶子节点的个数

实现思路

  • 首先，在上面小节 二叉树的特性 中我们推导出节点总数: n = n0 + n1 + n2
  • 然后，我们可以假设叶子节点总数为 n0，非叶子节点度为1的总数为 n1，非叶子节点度为2的总数为n2
  • 其次，我们通过小节 二叉树的特性 分析得出，n0 = n2 + 1，即 n2 = n0 - 1，所以 n = 2n0 + n1 - 1
  • 再次，在 完全二叉树特性 小节中我们分析了度为1的情况，即 n1 要么为1，要么0.
    • 如果 n1 为1，则 n 一定为偶数；n0 = n / 2; n1 + n2 = n / 2
    • 如果 n1 为0，则 n 一定为奇数。n0 = (n + 1) / 2；n1 + n2 = (n - 1) / 2
  • 最后，我们我们可以得出 n0（叶子节点） = 384

7. 参考博文