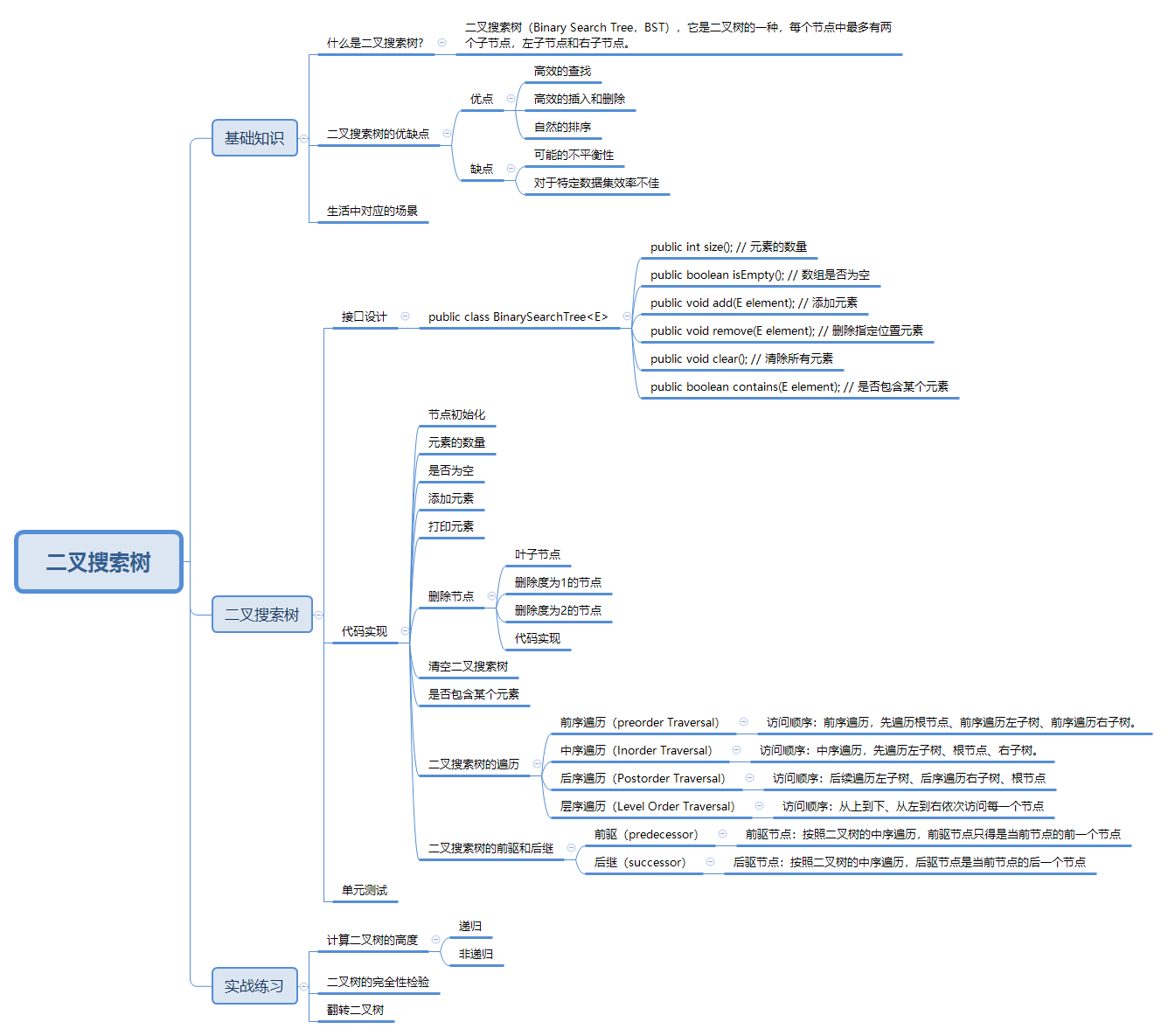
1. 内容大纲
本章节的代码:https://github.com/wicksonZhang/data-structure/tree/main/6-BST
2. 基础知识2.1. 什么是二叉搜索树
二叉搜索树(Binary Search Tree,BST):二叉搜索树是二叉树的一种,二叉搜索树中每个节点中最多有两个子节点,左子节点和右子节点。
其中任意一个节点的值都要 大于 其左子树所有节点的值
其中任意一个节点的值都要 小于 其右子树所有节点的值
它的左右子树也是一颗二叉搜索树
注意:二叉搜索树中存储的元素必须具备可比较性,且不允许为 null
2.2. 二叉搜索树解决了什么问题
如果从数组的角度进行考虑,数组如果添加、删除、查找元素的话,最好可能是 O(1) ,最坏的情况可能是 O(n) ,平均是 O(n) 。
但二叉搜索树就进一步的解决了这个问题:
高效查找 :由于其有序性质,可以利用二分搜索的方式快速定位到所需的节点,平均时间复杂度为 O(log n)。有序性: BST 中的节点按照特定的顺序排列。左子树的所有节点的值都小于根节点的值,右子树的所有节点的值都大于根节点的值。插入和删除操作: BST 允许相对快速地执行插入和删除操作。通过维护树的结构,并根据节点值的大小关系进行调整,可以在平均情况下以 O(log n)
2.3. 二叉搜索树的优缺点优点
高效的查找:BST 的结构使得查找操作高效,平均情况下时间复杂度为 O(log n),其中 n 是节点数量。
高效的插入和删除: 在大部分情况下,插入和删除操作的时间复杂度也为 O(log n),使得动态数据集的维护更为高效。
自然的排序:BST 的结构使得它天然具有排序性质,中序遍历 BST 可以得到有序的节点序列。
缺点
可能的不平衡性:在某些情况下,BST 可能会出现不平衡的情况,即树的高度会退化为接近线性,这会导致查找、插入和删除操作的最坏情况时间复杂度为 O(n) ,而非理想的 O(log n) 。
对于特定数据集效率不佳:如果数据集的顺序已经排好或者是逆序的,BST 的性能可能会大幅下降,因为它可能退化为链表形式,导致所有操作的时间复杂度都较高。
2.4. 生活中对应的场景
文件系统:在文件系统中,可以使用二叉树来存储目录和文件的关系。
检索数据:二叉搜索树是一种特殊的二叉树,可以用于快速检索数据 。
3. 接口设计1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class BinarySearchTree <E> { public int size () {} public boolean isEmpty () {} public void add (E element) {} public void remove (E element) {} public void clear () {} public boolean contains (E element) {} }
4. 代码实现4.1. 初始化成员变量1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 public class BinarySearchTree <E> { private int size; private Node<E> root; private static class Node <E> { E element; Node<E> rightNode; Node<E> leftNode; Node<E> parentNode; public Node (E element, Node<E> parentNode) { this .element = element; this .parentNode = parentNode; } public boolean isLeaf () { return leftNode == null && rightNode == null ; } public boolean hasTwoChildren () { return leftNode != null && rightNode != null ; } } }
4.2. 初始化构造器
注意:由于二叉搜索树中必须遵循两个值具备可比较性。针对这种情况我们采用了两种解决方案:
创建类并实现 Comparable 接口:class Person implements Comparable<Person>
自定义实现规则并实现 Comparator 接口:new BinarySearchTree<>(Comparator.comparingInt(Person::getAge))
1 2 3 4 5 6 7 8 9 10 11 12 13 public class BinarySearchTree <E> { private final Comparator<? super E> comparator; public BinarySearchTree () { this (null ); } public BinarySearchTree (Comparator<? super E> comparator) { this .comparator = comparator; } }
4.3. 元素的数量1 2 3 4 5 6 7 8 public int size () { return size; }
4.4. 是否为空1 2 3 4 5 6 7 8 public boolean isEmpty () { return size == 0 ; }
4.5. 添加元素
添加元素可能需要考虑的问题较多,而是二叉搜索树中必须满足如下两个条件
二叉搜索树中存储的元素必须具备可比较性,且不允许为 null。
二叉搜索树中左子节点的值必须要比当前节点小,右子节点的值必须比当前节点大。
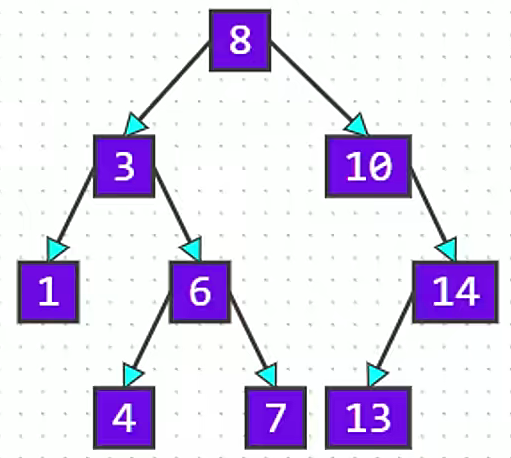
例如,下图中当根节点为空时,当前新添加的元素就是根节点。
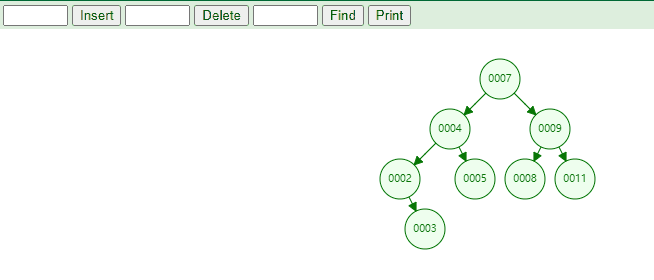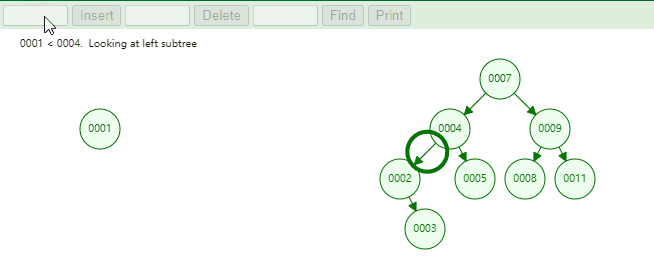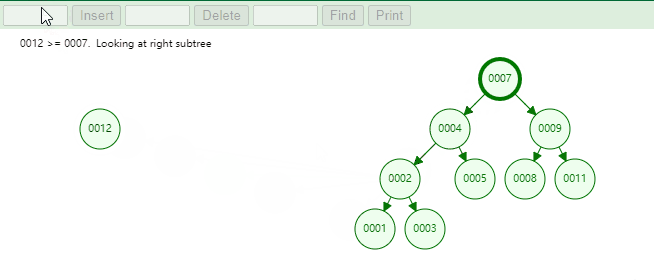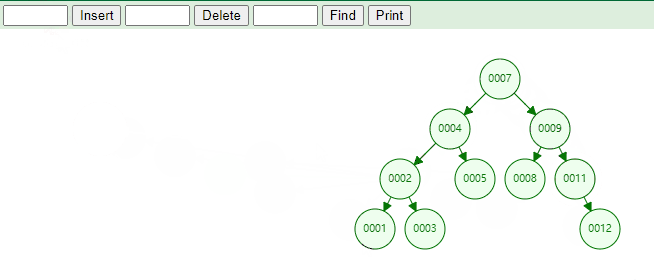
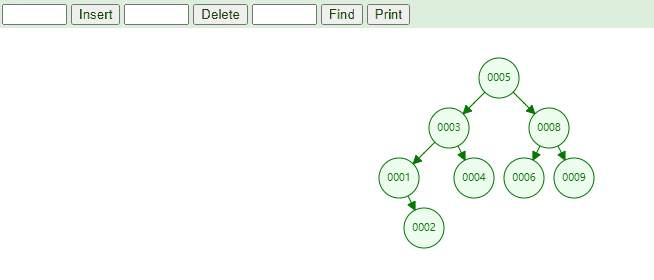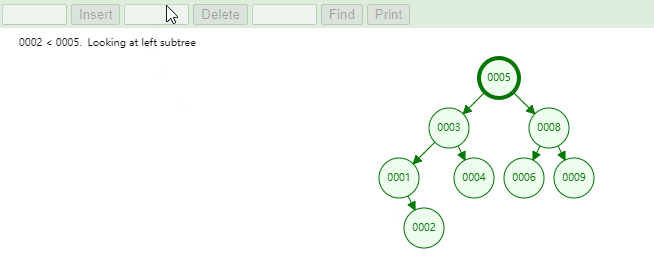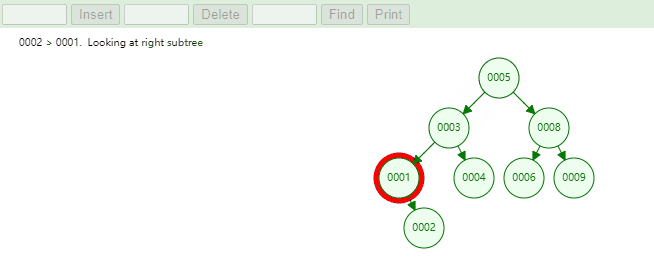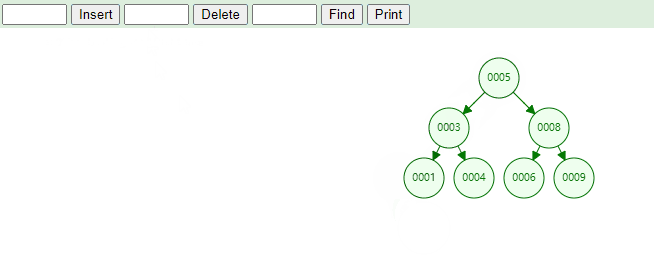
例如,下图中当根节点不为空时,我们需要添加元素为 1 和元素为 12 的节点。
实现思路:
Step1:判断当前节点是否为 root 根节点,如果是根节点直接进行插入。Step2:如果不为根节点,则找到当前元素需要添加的父级节点,如果小于则在左边,大于则在右边,等于则进行覆盖。Step3:通过找到的父级节点于当前元素比较的大小来判断,是添加在父级节点的左边还是右边。注意: 我们需要注意我们对元素进行比较时需要考虑两种情况。分别是 Comparator、Comparable 两种方式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public void add (E element) { checkedElementNotNull(element); if (root == null ) { root = new Node <>(element, null ); size++; return ; } Node<E> node = root; Node<E> parent = root; int cmp = 0 ; while (node != null ) { cmp = compare(element, node.element); parent = node; if (cmp > 0 ) { node = node.rightNode; } else if (cmp < 0 ) { node = node.leftNode; } else { node.element = element; return ; } } Node<E> newNode = new Node <>(element, parent); if (cmp > 0 ) { parent.rightNode = newNode; } else { parent.leftNode = newNode; } size++; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 @SuppressWarnings("unchecked") private int compare (E element1, E element2) { if (comparator != null ) { return comparator.compare(element1, element2); } return ((Comparable<E>) element1).compareTo(element2); }
4.6. 是否包含某个元素1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public boolean contains (E element) { return node(element) != null ; } private Node<E> node (E element) { Node<E> node = this .root; while (node != null ) { int cmp = compare(element, node.element); if (cmp > 0 ) { node = node.rightNode; } else if (cmp < 0 ) { node = node.leftNode; } else { return node; } } return null ; }
4.7. 二叉搜索树的遍历二叉搜索树的遍历主要分为以下四种:
前序遍历(Preorder Traversal)
中序遍历(Inorder Traversal)
后序遍历(Postorder Traversal)
层序遍历(Level Order Traversal)
4.7.1. 前序遍历(Preorder Traversal)前序遍历顺序:前序遍历先遍历根节点、左子树、右子树。
下图的访问节点顺序:7、4、2、1、3、5、9、8、11、10、12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public void preorderTraversal () { preorderTraversal(root); } private void preorderTraversal (Node<E> node) { if (node == null ) { return ; } System.out.println("node.element = " + node.element); preorderTraversal(node.leftNode); preorderTraversal(node.rightNode); }
4.7.2. 中序遍历(Inorder Traversal)中序遍历顺序:中序遍历先遍历左子树、根节点、右子树。
下图的访问节点结果:1、2、3、4、5、6、7、8、9、10、11、12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public void inorderTraversal () { inorderTraversal(root); } private void inorderTraversal (Node<E> node) { if (node == null ) { return ; } inorderTraversal(node.leftNode); System.out.println("node.element = " + node.element); inorderTraversal(node.rightNode); }
4.7.3. 后序遍历(Postorder Traversal)后序遍历顺序:后续遍历先遍历左子树、右子树、根节点
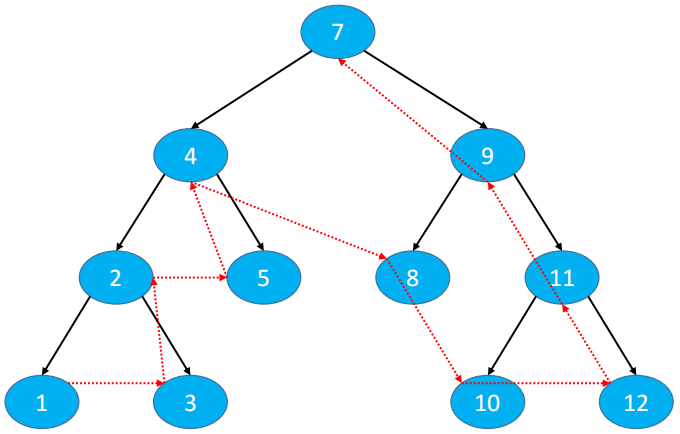
下图的访问节点顺序:1、3、2、5、4、8、10、12、11、9、7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public void postOrderTraversal () { postOrderTraversal(root); } private void postOrderTraversal (Node<E> node) { if (node == null ) { return ; } postOrderTraversal(node.leftNode); postOrderTraversal(node.rightNode); System.out.println("node.element = " + node.element); }
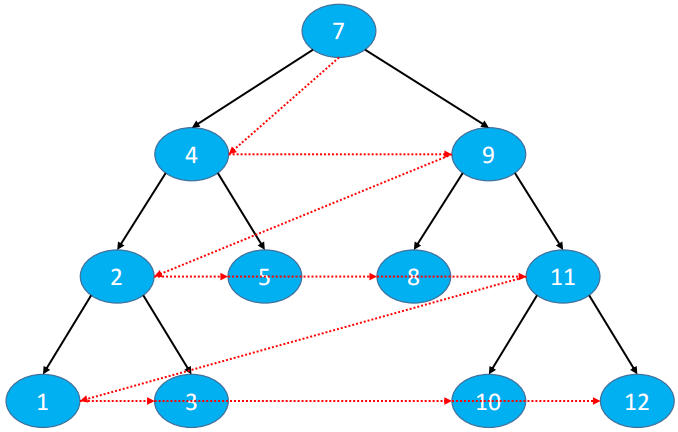
4.7.4. 层序遍历(Level Order Traversal)层序遍历顺序:从上到下、从左到右依次访问每一个节点
下图的访问节点顺序:7、4、9、2、5、8、11、1、3、10、12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public void levelOrderTraversal () { levelOrderTraversal(root); } private void levelOrderTraversal (Node<E> node) { if (node == null ) { return ; } Queue<Node<E>> queue = new LinkedList <>(); queue.offer(node); while (!queue.isEmpty()) { Node<E> newNode = queue.poll(); System.out.print("newNode = " + newNode.element); if (node.leftNode != null ) { queue.offer(node.leftNode); } if (node.rightNode != null ) { queue.offer(node.rightNode); } } }
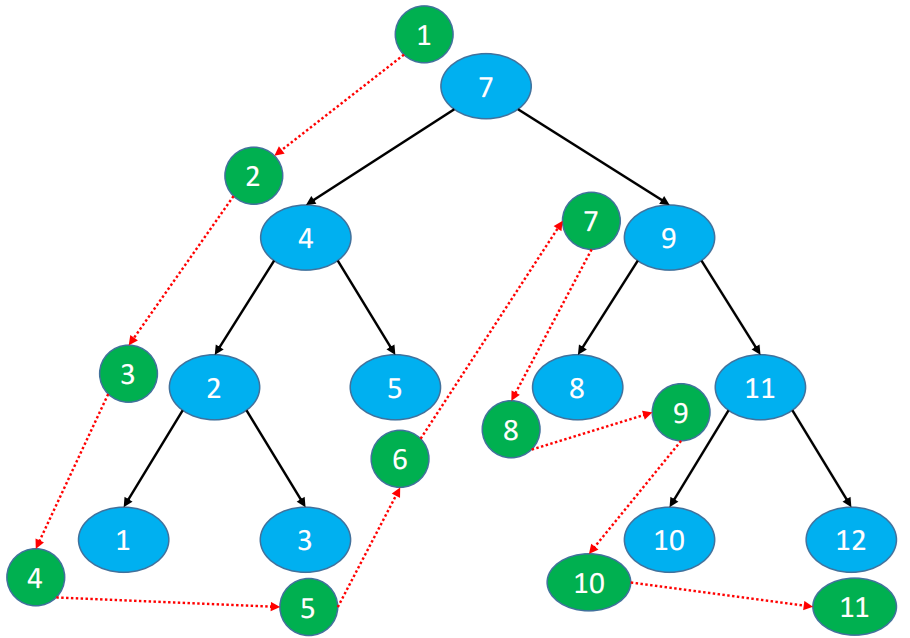
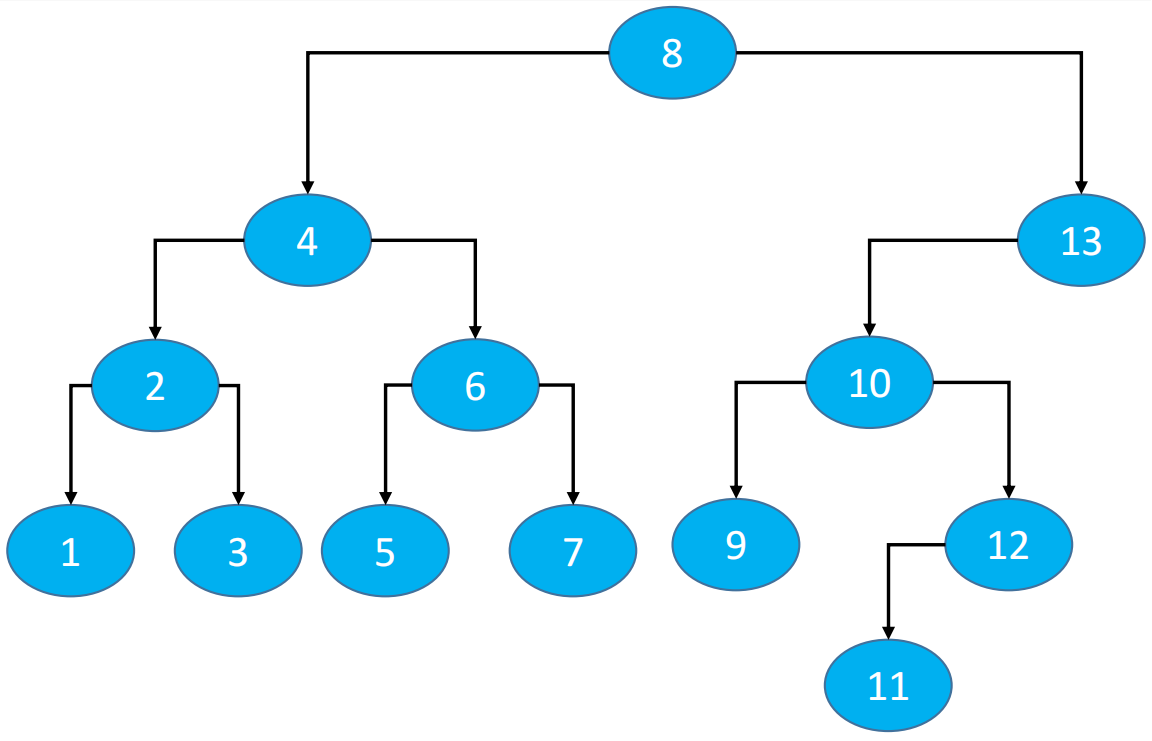
4.8. 二叉搜索树的前驱和后继4.8.1. 前驱(predecessor)前驱节点 :按照二叉树的中序遍历,前驱节点只得是当前节点的前一个节点。
基于中序访问节点顺序:1、2、3、4、5、6、7、8、9、10、11、12、13
例子:节点 8 的前驱节点就是 7
实现思路:
Step1:以节点 8 为例,如果需要找到节点 8 的前驱,需要经历如下步骤:
首先,找到当前节点的左子节点 Node<E> node = root.left(4)
然后,一直找左子节点的右子节点 node = node.right(6)
最后,判断叶子节点的右子节点为null(7)
Step2:以节点 9 为例,如果需要找到节点 9 的前驱,需要经历如下步骤:
首先,当前节点的左子节点一定为null,且父节点不为 null.
然后,一直找到当前节点的父级节点 node = node.parent(10,13)
最后,判断当前节点是不是在父级节点的左子节点 node == node.parent.left,如果是就一直找,如果不是就停止。
Step3:最后根据 Step2 的步骤进行返回相关结果集
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public Node<E> predecessor (Node<E> node) { if (node == null ) { return null ; } if (root.leftNode != null ) { Node<E> node1 = root.leftNode; while (node1.rightNode != null ) { node1 = node1.rightNode; } return node1; } Node<E> parentNode = node.parentNode; while (parentNode != null && node == parentNode.leftNode) { node = parentNode; parentNode = parentNode.parentNode; } return parentNode; }
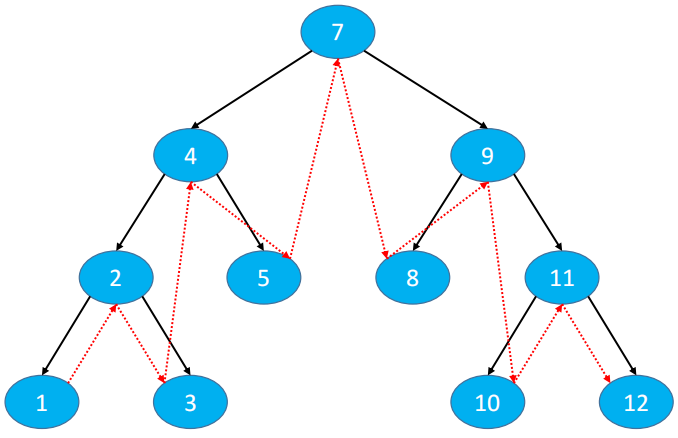
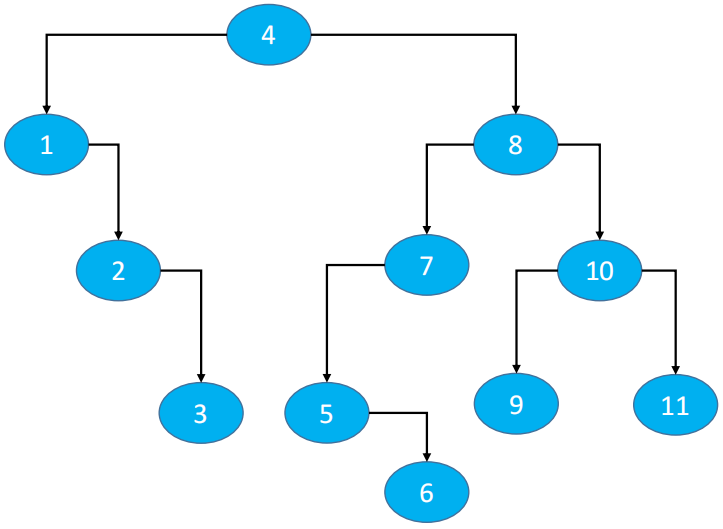
4.8.2. 后继(successor)后继节点 :按照二叉树的中序遍历,后继节点是当前节点的后一个节点。
基于中序访问节点顺序:1、2、3、4、5、6、7、8、9、10、11
例子:当前节点 4 的后继节点就是 5
实现思路:后序节点的实现思路本质上是与前序节点实现的思路逻辑是相反的。
Step1:以节点 4 为例,如果需要找到节点 4 的后继,需要经历如下步骤:
首先,找到当前节点的右子节点 Node<E> node = node.rightNode(8)
然后,一直找到右子节点的左子节点 node = node.leftNode(7)
最后,判断最后一个节点的左子节点是否为null(5)
Step2:以节点 3 为例,如果需要找到节点 4 的后继,需要经历如下步骤:
首先,当前节点的右子节点一定为 null,且父节点不为 null.
然后,一直找到当前节点的父级节点 node = node.parentNode.
最后,判断当前节点是不是在父级节点的右子节点 node == node.parent.rightNode,如果是就一直找,如果不是就停止。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public Node<E> successor (Node<E> node) { if (node == null ) { return null ; } if (root.rightNode != null ) { Node<E> rightNode = root.rightNode; while (rightNode.leftNode != null ) { rightNode = rightNode.leftNode; } return rightNode; } Node<E> parentNode = node.parentNode; while (parentNode != null && node == parentNode.rightNode) { node = parentNode; parentNode = parentNode.parentNode; } return parentNode; }
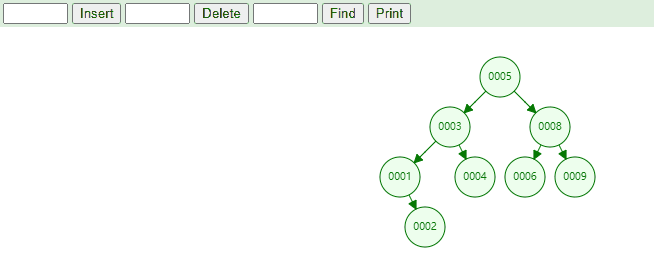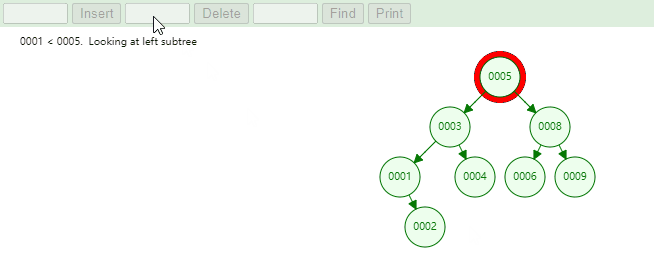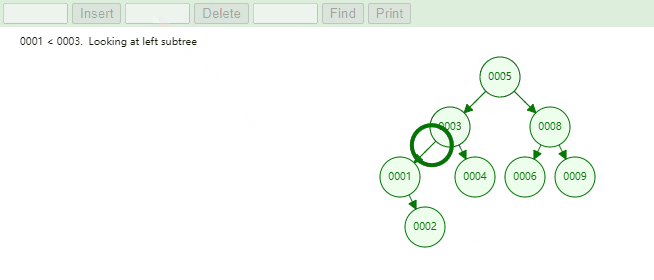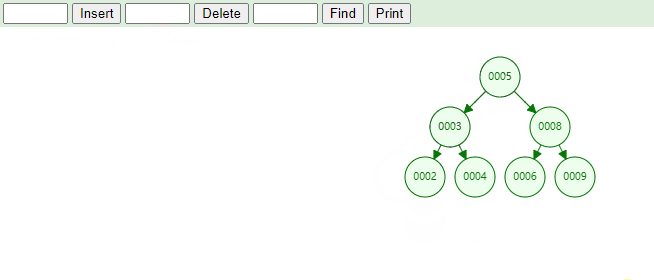
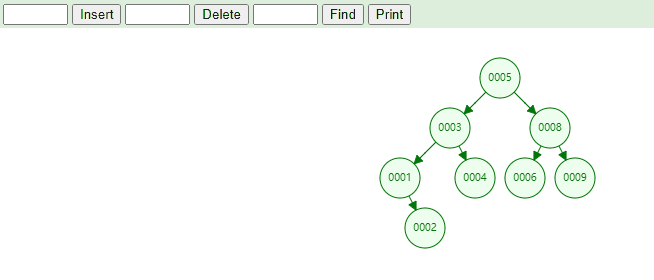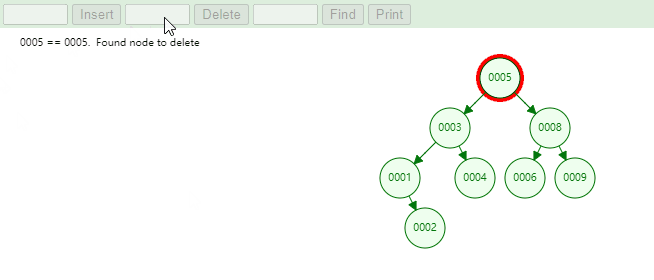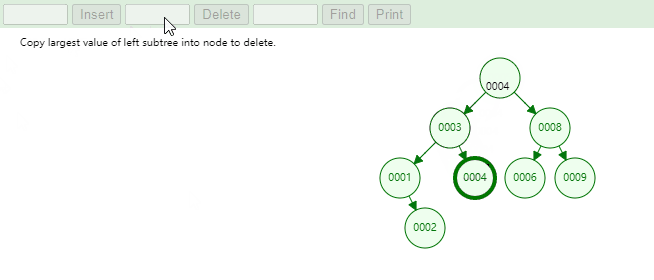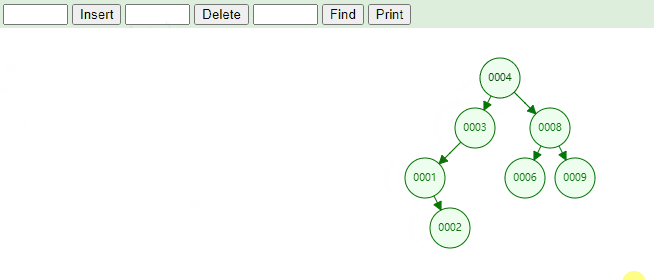
4.9. 删除元素删除元素:在二叉树搜索树中删除元素中可以分为三个部分:
删除叶子节点
删除度为1的节点
删除度为2的节点。
删除叶子节点,实现思路如下:
首先找到节点信息,判断节点是在左子节点还是右子节点,最后执行如下代码
node.parentNode.rightNode = null
注意:需要考虑只存在一个节点的情况,也就是根节点。
删除度为 1 的节点,实现思路如下:
当找到需要删除的节点后,判断当前节点是左子节点还是右子节点,最后执行如下代码
node.rightNode.parentNode = node.parentNode
node.parentNode.leftNode = node.rightNode
注意:这里如果根节点只存在一个度的情况
删除度为 2 的节点,实现思路如下:
当找到需要删除的节点后,本质上就是找到当前节点的前驱节点或者后继节点来覆盖掉当前节点的值,在删除叶子节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 private void remove (Node<E> node) { if (node == null ) { return ; } if (node.hasTwoChildren()) { Node<E> predecessorNode = predecessor(node); node.element = predecessorNode.element; node = predecessorNode; } Node<E> removeNode = node.leftNode != null ? node.leftNode : node.rightNode; if (removeNode != null ) { removeNode.parentNode = node.parentNode; if (removeNode.parentNode == null ) { root = removeNode; } else if (node == node.parentNode.leftNode) { node.parentNode.leftNode = removeNode; } else { node.parentNode.rightNode = removeNode; } } else if (node.parentNode == null ) { root = null ; } else { if (node == node.parentNode.leftNode) { node.parentNode.leftNode = null ; } else { node.parentNode.rightNode = null ; } } size--; }
4.10. 清空元素1 2 3 4 5 6 7 public void clear () { root = null ; size = 0 ; }
4.11. 单元测试1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 public class BinarySearchTreeTest { private BinarySearchTree<Integer> bst; @BeforeEach public void setup () { bst = new BinarySearchTree <>(); bst.add(5 ); bst.add(3 ); bst.add(7 ); bst.add(2 ); bst.add(4 ); bst.add(6 ); bst.add(8 ); } @Test public void testSize () { Assertions.assertEquals(7 , bst.size()); bst.remove(3 ); Assertions.assertEquals(6 , bst.size()); } @Test public void testIsEmpty () { Assertions.assertFalse(bst.isEmpty()); bst.clear(); Assertions.assertTrue(bst.isEmpty()); } @Test public void testAdd () { bst.add(9 ); Assertions.assertTrue(bst.contains(9 )); } @Test public void testRemove () { Assertions.assertTrue(bst.contains(3 )); bst.remove(3 ); Assertions.assertFalse(bst.contains(3 )); } @Test public void testContains () { Assertions.assertTrue(bst.contains(7 )); Assertions.assertFalse(bst.contains(10 )); } @Test public void testPreorderTraversal () { StringBuilder sb = new StringBuilder (); System.setOut(new java .io.PrintStream(System.out) { @Override public void println (String x) { sb.append(x).append("\n" ); } }); bst.preorderTraversal(); Assertions.assertEquals("node.element = 5\nnode.element = 3\nnode.element = 2\nnode.element = 4\nnode.element = 7\nnode.element = 6\nnode.element = 8\n" , sb.toString()); } @Test public void testCustomComparator () { BinarySearchTree<String> stringBST = new BinarySearchTree <>(Comparator.reverseOrder()); stringBST.add("apple" ); stringBST.add("banana" ); stringBST.add("cherry" ); StringBuilder sb = new StringBuilder (); System.setOut(new java .io.PrintStream(System.out) { @Override public void println (String x) { sb.append(x).append("\n" ); } }); stringBST.inorderTraversal(); Assertions.assertEquals("node.element = cherry\nnode.element = banana\nnode.element = apple\n" , sb.toString()); } }
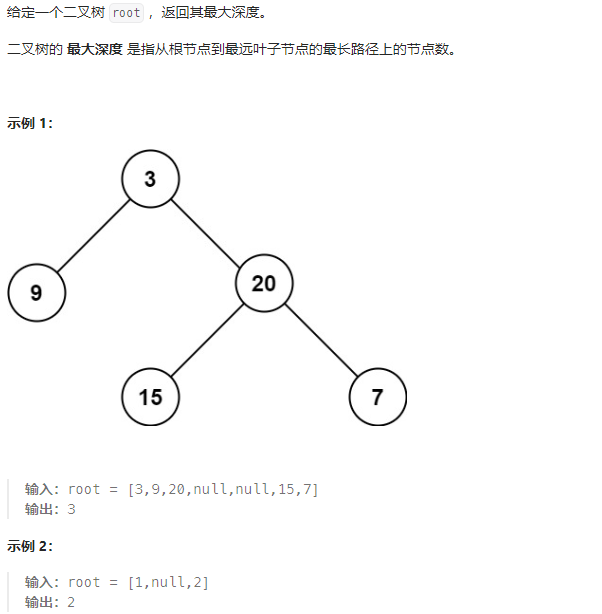
5. 实战练习5.1. 二叉树的最大深度
二叉树的最大深度:https://leetcode.cn/problems/maximum-depth-of-binary-tree/
需求 :
5.1.1. 递归实现
采用递归实现思路
假设,左子节点有两层,我们采用递归进行遍历。结束的方法是 根节点为 null 就返回0.
如果一个节点没有子节点,它的高度就是1(根节点高度为1)。
如果一个节点有一个子节点,那么它的高度就是子节点的高度加1。
实现代码
1 2 3 4 5 6 public int maxDepth (TreeNode root) { if (root == null ) { return 0 ; } return 1 + Math.max(maxDepth(root.left), maxDepth(root.right)); }
5.1.2. 非递归实现
采用层序遍历实现树的最大深度
实现思路
首先,第一层节点进行入队,也就是节点 7,队列里面只有一个元素,这是第一层
然后,当节点 7 出队时,第二层节点(4,9)在进行入队,队列里面只有二个元素,这是第二层
最后,当第二层的节点出队时,第三层节点(2,5,8,11)的节点在进行入队,队列里面只有二个元素,这是第三层。
如果当队列中元素为 0 就表示所有的节点遍历完了
实现代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 private int height (Node<E> node) { if (node == null ) { return 0 ; } int height = 0 ; int levelSize = 1 ; Queue<Node<E>> queue = new LinkedList <>(); queue.offer(node); while (!queue.isEmpty()) { Node<E> poll = queue.poll(); levelSize--; if (poll.leftNode != null ) { queue.offer(poll.leftNode); } if (poll.rightNode != null ) { queue.offer(poll.rightNode); } if (levelSize == 0 ) { levelSize = queue.size(); height++; } } return height; }
5.2. 二叉树的完全性检验
地址:https://leetcode.cn/problems/check-completeness-of-a-binary-tree/
需求
代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public boolean isCompleteTree (TreeNode root) { if (root == null ) { return false ; } boolean leaf = false ; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode poll = queue.poll(); if (poll.left != null ) { queue.offer(poll.left); } else if (poll.right != null ) { return false ; } if (poll.right != null ) { queue.offer(poll.right); } else { leaf = true ; } } return leaf; }
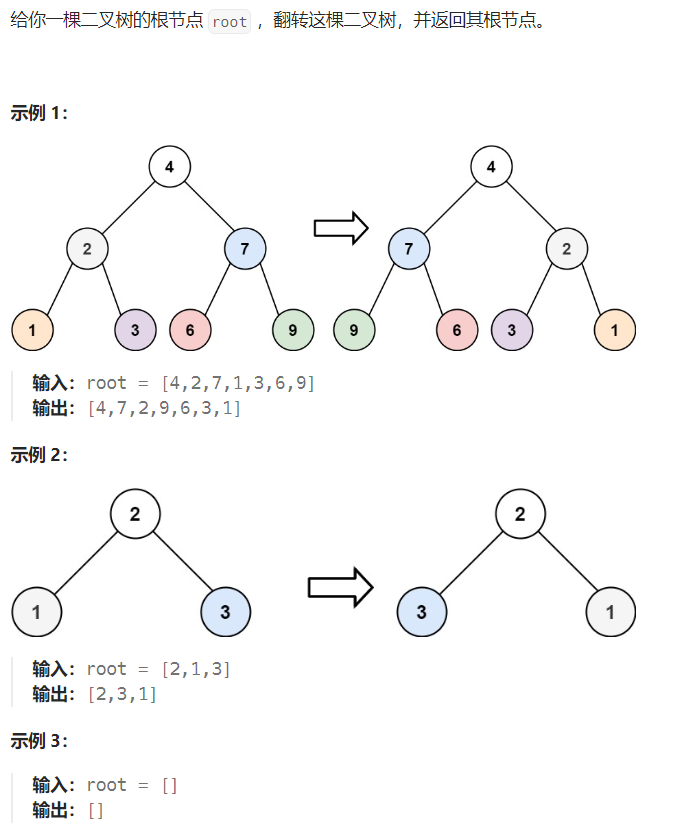
5.3. 翻转二叉树
地址:https://leetcode.cn/problems/invert-binary-tree/description/
需求
代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 public TreeNode invertTree (TreeNode root) { if (root == null ) { return null ; } TreeNode treeNode = root.right; root.right = root.left; root.left = treeNode; invertTree(root.left); invertTree(root.right); return root; }
6. 参考博文