数据结构-平衡二叉树

1. 内容大纲

本章节代码：https://github.com/wicksonZhang/data-structure/tree/main/7-AVL

---

2. 基础知识

2.1. 什么是平衡二叉树

平衡二叉树也被称为 AVL 树，是一种树形结构的数据结构，为了保持平衡，它的核心是左右子树高度不能相差1的二叉树。

2.2. 平衡二叉树解决了什么问题

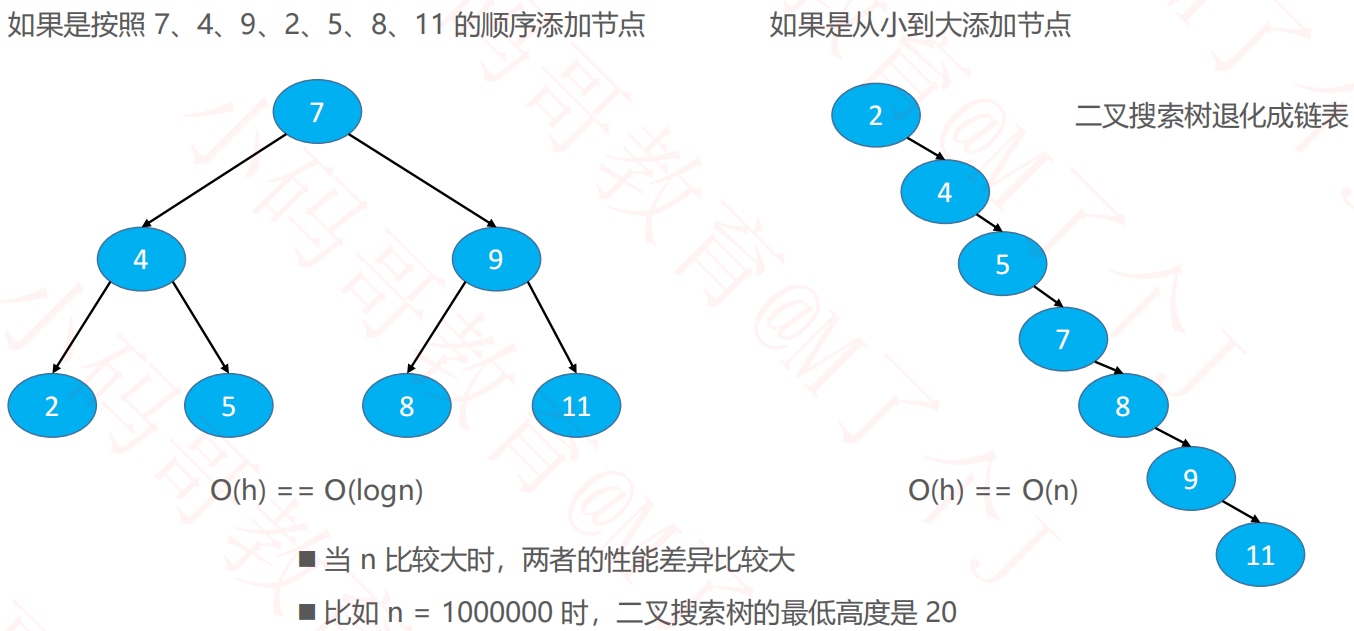
1. 平衡二叉树主要解决的是 二叉搜索树 性能退化的问题。

2. 在普通二叉搜索树中，如果数据按照某种顺序插入或者删除时，会导致树退回为链表，直接导致查询、删除的时间复杂度变为 O(n)。

• 如下图中就是二叉搜索树退回为了链表

  

2.3. 平衡二叉树的优缺点

优点

1. 快速的查找、插入和删除：由于AVL维持了较低的高度，使得查找、插入和删除操作的时间复杂度始终保持在O(log n)。
2. 平衡性的文档：AVL树保证了树的平衡性，每个节点的左右子树高度差不超过1，这确保了在各种操作下的稳定性和高效性。

缺点

1. 复杂的代码：由于需要维护平衡性，则插入和删除需要执行树的旋转来维持平衡，这些操作会增加算法的复杂度和开销。
2. 额外的空间开销：每个节点需要额外的空间来存储平衡因子或者其他信息来维护树的平衡性，这会增加内存开销。
3. 不适合频繁插入、删除操作的场景： 如果应用程序的主要操作是频繁的插入和删除，而不是查找操作，AVL树可能不是最佳选择。因为频繁的旋转操作可能会导致性能下降，其他数据结构（比如跳表或者B树）可能更适合这种情况。

2.4. 生活中对应的场景

• Windows对进程地址空间的管理用到了AVL

---

3. 二叉树失衡的情况

3.1. 添加导致的失衡

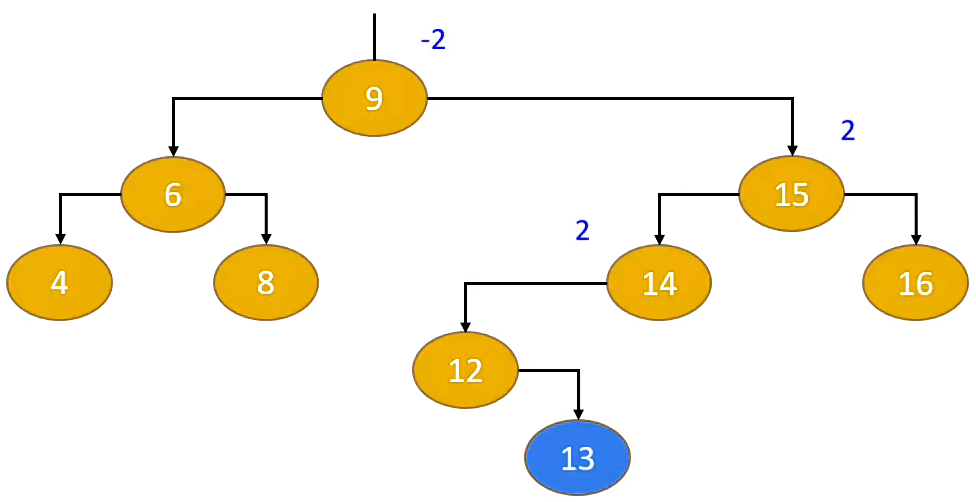
• 如下图中，当添加 13 这个节点时，会导致祖先节点进行失衡。

  

3.2. 添加导致的失衡的解决方案

目前添加导致的失衡存在如下四种情况：

• LL - 右旋转（单旋）
• RR - 左旋转（单旋）
• LR - RR 左旋转，LL右旋转（双旋）
• RL - LL 右旋转，RR左旋转（双旋）

3.2.1. LL - 右旋转（单旋）

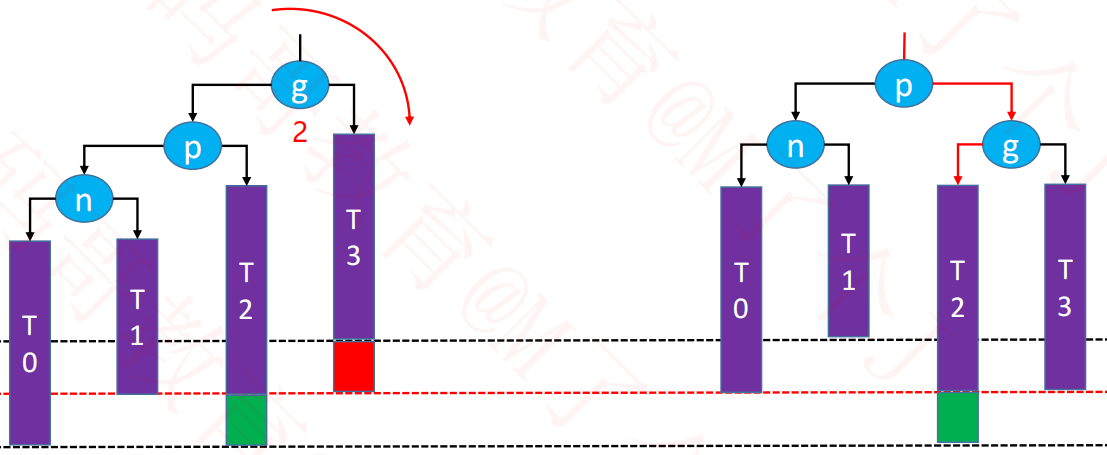
如下图中，其中 n 代表 node ，p 代表 parent ，g 代表 grandparent。

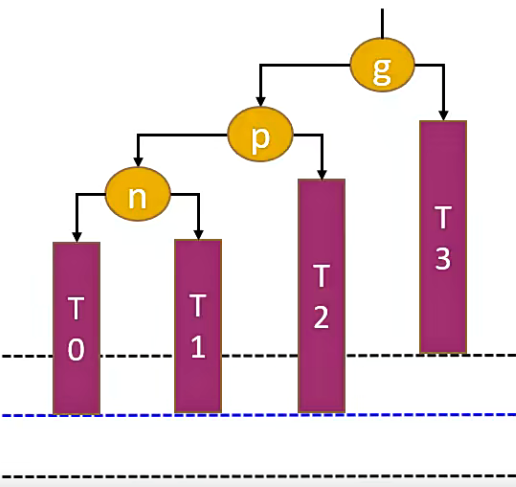
当需要在节点 n 的左子树 T0 中添加元素，则会导致节点 g 失衡。

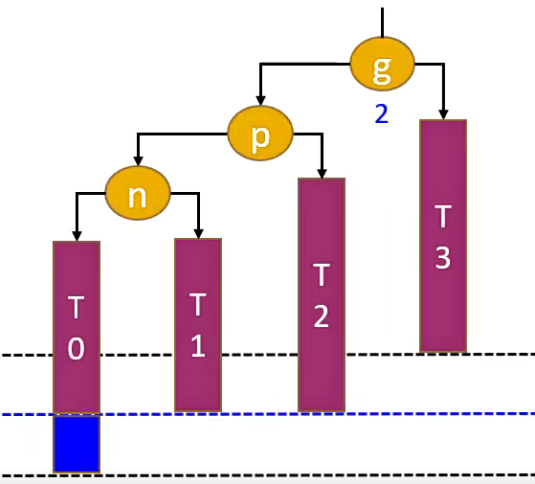
当节点 g 左边的左边节点失去平衡时，我们称这种情况为 LL。针对这种情况我们需要进行右旋转，具体如下图。

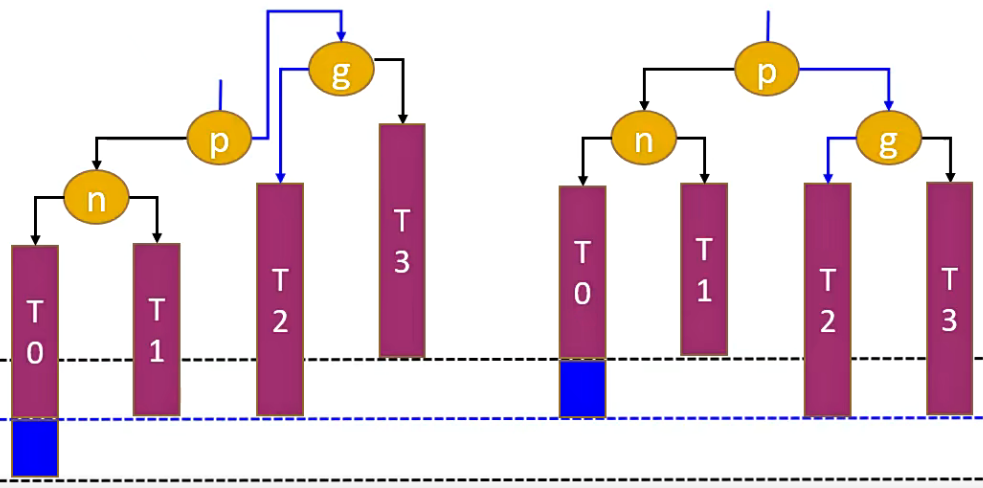
解决思路（右旋转）

• 首先，我们将节点 g 的左子树指向节点 p 的右子树，即：g.left = p.right。
• 然后，再将节点 p 的右子树指向节点 g ，即：p.right = g。
• 最后，让节点 p 成为这颗子树的根节点。
• 当修改完成之后这仍然是一颗二叉搜索树：T0 < n < T1 < p < T2 < g < T3。

注意事项

• T2、p、g 的 parent 属性
• 更新 g、p 的高度

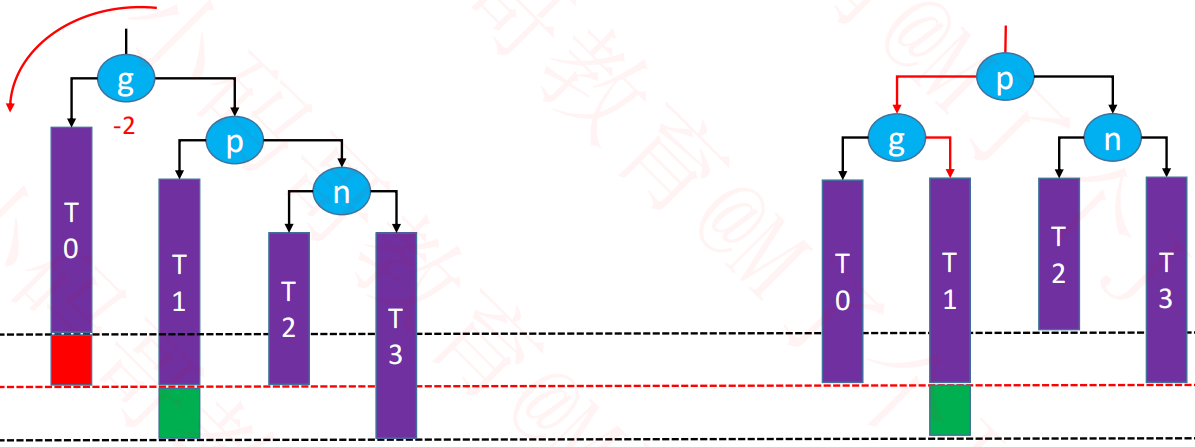
3.2.2. RR - 左旋转（单旋）

现在需要在节点 n 的左子树或者右子树 T2、T3 中添加元素，则会导致节点 g 失衡。

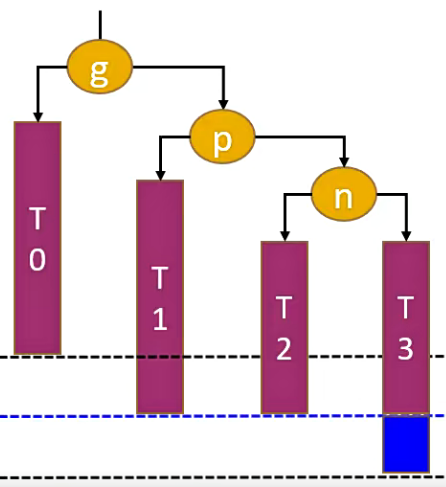
当节点 g 右边的右边节点失去平衡时，我们称这种情况为 RR。针对这种情况我们需要进行左旋转，具体如下图。

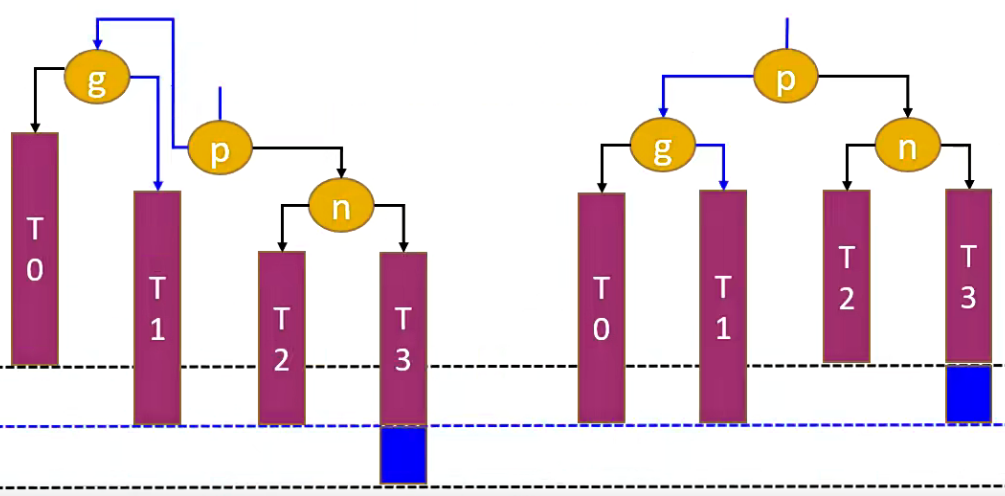
解决思路（左旋转）

• 首先，我们将节点 g 的右子树指向节点 p 的左子树，即：g.right= p.left。
• 然后，再将节点 p 的左子树指向节点 g ，即：p.left= g。
• 最后，让节点 p 成为这颗子树的根节点。
• 当修改完成之后这仍然是一颗二叉搜索树：T0 < g < T1 < p < T2 < g < T3。

注意事项

• T3、p、g 的 parent 属性。
• 更新 g、p 的高度。

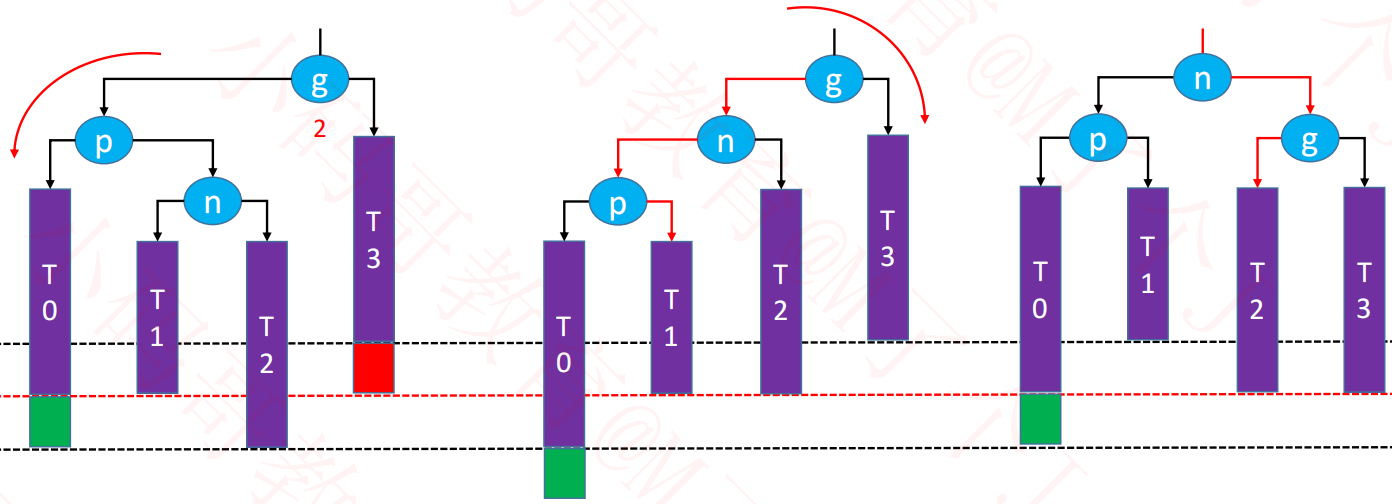
3.2.3. LR - RR 左旋转，LL右旋转（双旋）

当节点 p 是 节点 g 的 left 节点，节点 n 是 节点 p 的 right 节点，现在往节点 n 添加节点，这种情况称为 LR。

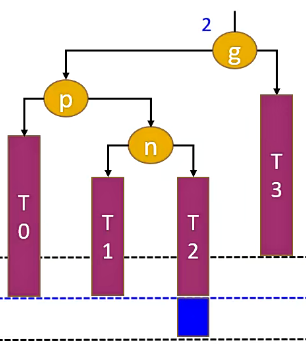
如果是 LR，我们先进行一次左旋转，将二叉树变为 LL。

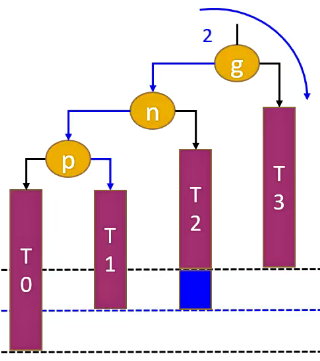
然后再进行一次右旋转，即可使树达到平衡。

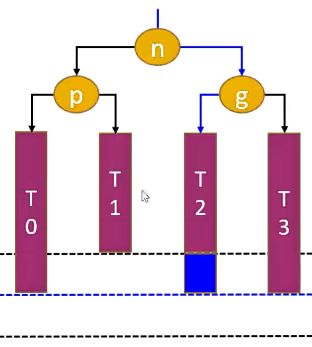
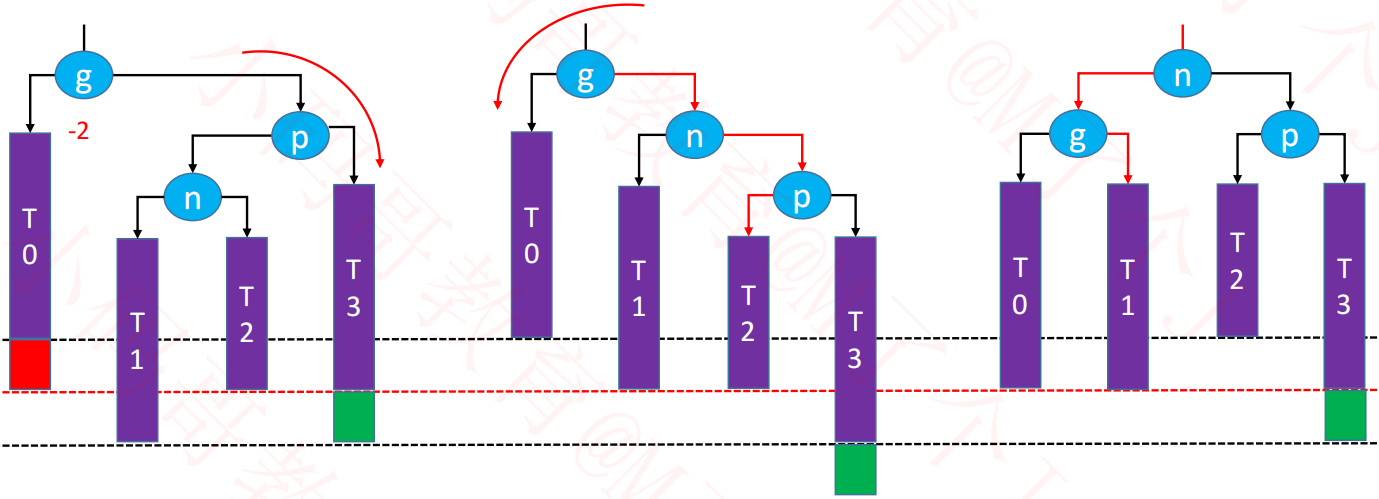
3.2.4. RL - LL 右旋转，RR左旋转（双旋）

当节点 p 是 节点 g 的 right 节点，节点 n 是 节点 p 的 left 节点，现在往 节点 n 添加节点，这种情况称为 RL。

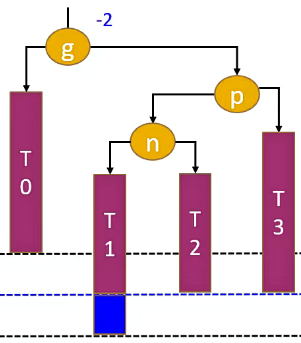
如果是 RL，我们先进行一次右旋转，将二叉树变为 RR。

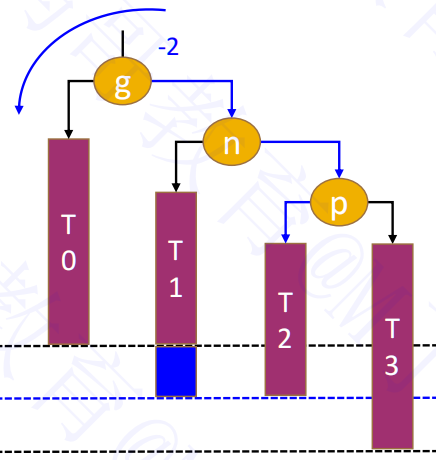
然后再进行左旋转，即可达到平衡。

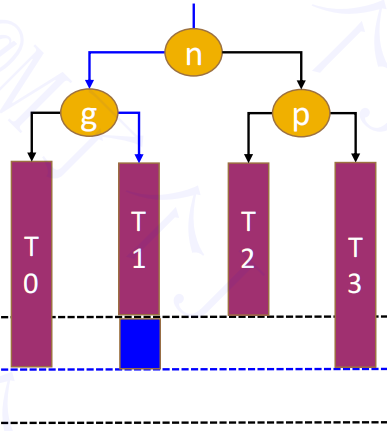
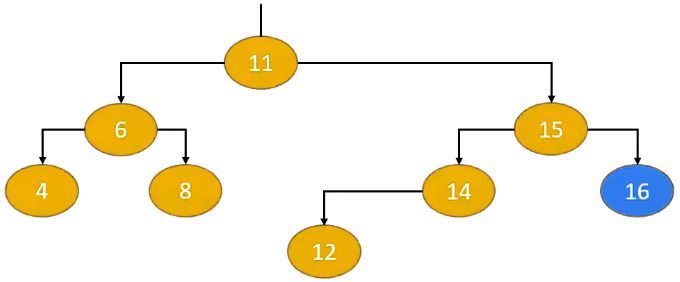
3.3. 删除导致的失衡

• 例如，当我们需要删除如下二叉树中的节点（16）时，会导致父节点进行失衡。

3.4. 删除导致的失衡的解决方案

• 删除导致的失衡和添加导致的失衡需要考虑的情况是差不多的

3.4.1. LL - 右旋转（单旋）

3.4.2. RR - 左旋转（单旋）

3.4.3. LR - RR 左旋转，LL右旋转（双旋）

3.4.4. RL - LL 右旋转，RR左旋转（双旋）

---

4. 平衡二叉树

4.1. UML 类图

• 平衡二叉树是在 二叉搜索树 基础上进行开发的，如下是 UML 类图。

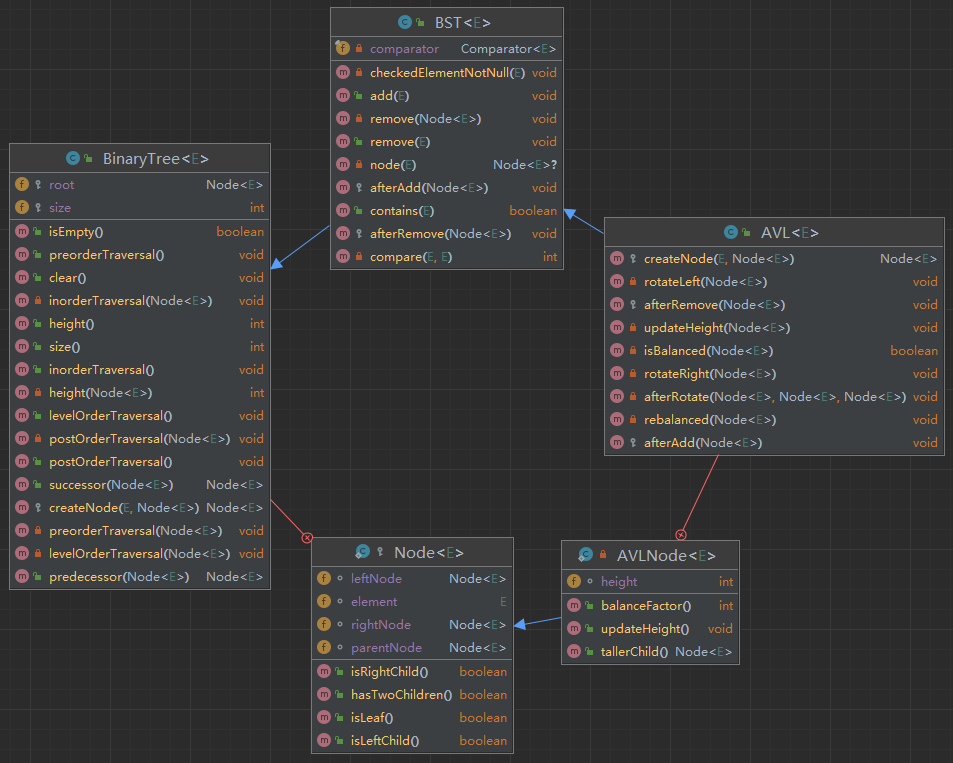
4.2. 代码实现

• 我们平衡二叉树是基于二叉搜索树进行开发，所以当我们的二叉搜索树添加完节点之后，如果当前二叉树失衡之后，我们需要恢复平衡。具体操作如下图

  

• 实现的思路如下（我们的代码就是基于如下思路进行开发）

  • 首先，我们基于 BST 进行开发，当我们新添加元素时需要保证 AVL 和 BST 互不影响。
  • 其次，当 AVL 添加时需要判断当前树是否处于平衡状态。
  • 然后，如果这棵树处于平衡状态我们则更新这颗树的高度。
  • 最后，如果当前树不处于平衡状态时需要重新让这棵树处于平衡。

4.2.1. 添加节点 - afterAdd()

• 我们基于 BST 进行开发，当我们新添加元素时需要保证 AVL 和 BST 互不影响。

  • 我们需要在 BST.java 中修改 add() ，如果是基于 AVL 那么则需要进行添加节点之后进行处理。

  /**
   * 添加元素
   *
   * @param element 元素
   */
  public void add(E element) {
      // 参数检查
      checkedElementNotNull(element);
    
      // 如果当前的父级节点为 null ，则代表添加第一个元素
      if (root == null) {
          // TODO ...
          // 新添加节点之后处理
          afterAdd(root);
          return;
      }
    
      // 如果当前的父级节点不为 null ,我们将需要添加的元素添加在父级节点的那个位置
      Node<E> newNode = createNode(element, parent);
      // TODO ...
      afterAdd(newNode);
  }
    
  /**
   * 添加节点之后进行调整
   *
   * @param node 节点信息
   */
  protected void afterAdd(Node<E> node) { }

  • 由于 AVL.java 继承了 BST.java 所以在 BST 中需要重写 afterAdd()

  @Override
  protected void afterAdd(Node<E> node) {
      while ((node = node.parentNode) != null) {
          // 判断整棵树是否平衡，如果平衡，则更新高度，如果不平衡，则恢复平衡
          if (isBalanced(node)) {
              // 更新高度
              updateHeight(node);
          } else {
              // 恢复平衡
              rebalanced(node);
              break;
          }
      }
  }

4.2.2. 是否平衡 - isBalanced()

• 当 AVL 添加时需要基于平衡因子判断当前树是否处于平衡状态，具体的思路就是判断左右子树的高度是否小于等于1

  • 我们判断是否处于平衡，主要是在 isBalanced(Node<E> node) 中进行判断

  /**
   * 判断是否平衡
   *
   * @param node 节点
   * @return boolean
   */
  private boolean isBalanced(Node<E> node) {
      return Math.abs(((AVLNode<E>) node).balanceFactor()) <= 1;
  }

  • 其中 AVLNode<E> 主要是针对我们平衡二叉树进行使用与 BST 无关

  /**
   * AVL 节点信息
   *
   * @param <E>
   */
  private static class AVLNode<E> extends Node<E> {
      int height = 1;
    
      public AVLNode(E element, Node<E> parentNode) {
          super(element, parentNode);
      }
    
      /**
       * 平衡因子
       *
       * @return int
       */
      public int balanceFactor() {
          int leftHeight = leftNode == null ? 0 : ((AVLNode<E>) leftNode).height;
          int rightHeight = rightNode == null ? 0 : ((AVLNode<E>) rightNode).height;
          return leftHeight - rightHeight;
      }
    
  }

4.2.3. 更新高度 - updateHeight()

• 如果这棵树处于平衡状态我们则更新这颗树的高度，具体的思路就是当前节点的父级节点的高度

  • 我们更新高度主要在 updateHeight(Node<E> node) 中进行

  /**
   * 更新节点高度
   *
   * @param node 节点
   */
  private void updateHeight(Node<E> node) {
      ((AVLNode<E>) node).updateHeight();
  }

  • 其中更新高度的方法 updateHeight() 在 AVLNode<E> 中进行封装即可，树的高度等于左右子树中的最大值 + 1

  /**
   * AVL 节点信息
   *
   * @param <E>
   */
  private static class AVLNode<E> extends Node<E> {
      int height = 1;
    
      public AVLNode(E element, Node<E> parentNode) {
          super(element, parentNode);
      }
      
      // TODO ...
    
      /**
       * 更新高度
       */
      public void updateHeight() {
          int leftHeight = leftNode == null ? 0 : ((AVLNode<E>) leftNode).height;
          int rightHeight = rightNode == null ? 0 : ((AVLNode<E>) rightNode).height;
          height = 1 + Math.max(leftHeight, rightHeight);
      }
    
  }

4.2.4. 恢复平衡 - rebalanced()

• 如果当前树处于不平衡状态时需要重新让这棵树处于平衡，具体的思路请看 《添加导致的失衡的解决方案》

  • 如果当前树处于不平衡状态，主要是在 rebalanced(Node<E> node) 中进行判断

  /**
   * 重新恢复平衡
   *
   * @param grand 节点
   */
  private void rebalanced(Node<E> grand) {
      Node<E> parent = ((AVLNode<E>) grand).tallerChild();
      Node<E> node = ((AVLNode<E>) parent).tallerChild();
      // parent 是 grand 的左子树
      if (parent.isLeftChild()) { // L
          if (node.isLeftChild()) { // LL
              rotateRight(grand);
          } else { // LR
              rotateLeft(parent);
              rotateRight(grand);
          }
      } else { // R
          if (node.isLeftChild()) { // RL
              rotateRight(parent);
              rotateLeft(grand);
          } else { // RR
              rotateLeft(grand);
          }
      }
  }

  • 其中在 AVLNode<E> 中获取高度比较高的子节点

  /**
   * AVL 节点信息
   *
   * @param <E>
   */
  private static class AVLNode<E> extends Node<E> {
      int height = 1;
    
      public AVLNode(E element, Node<E> parentNode) {
          super(element, parentNode);
      }
    
      // TODO ...
    
      /**
       * 高度比较高的子节点
       *
       * @return Node<E>
       */
      public Node<E> tallerChild() {
          int leftHeight = leftNode == null ? 0 : ((AVLNode<E>) leftNode).height;
          int rightHeight = rightNode == null ? 0 : ((AVLNode<E>) rightNode).height;
          // 左子树高，就返回左子树
          if (leftHeight > rightHeight) return leftNode;
          // 右子树高，就返回右子树
          if (leftHeight < rightHeight) return rightNode;
          return isLeftChild() ? leftNode : rightNode;
      }
    
  }

  • 左旋和右旋的相关代码

  /**
   * 左旋转
   *
   * @param grand 节点
   */
  private void rotateLeft(Node<E> grand) {
      Node<E> parent = grand.rightNode;
      Node<E> child = parent.leftNode;
      grand.rightNode = child;
      parent.leftNode = grand;
      afterRotate(grand, parent, child);
  }
    
  /**
   * 右旋转
   *
   * @param grand 节点
   */
  private void rotateRight(Node<E> grand) {
      Node<E> parent = grand.leftNode;
      Node<E> child = parent.rightNode;
      grand.leftNode = child;
      parent.rightNode = grand;
      afterRotate(grand, parent, child);
  }
    
  private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) {
      // 让 parent 成为子树的根节点
      parent.parentNode = grand.parentNode;
      if (grand.isLeftChild()) {
          grand.parentNode.leftNode = parent;
      } else if (grand.isLeftChild()) {
          grand.parentNode.leftNode = parent;
      } else {
          root = parent;
      }
    
      // 更新 child 的parent
      if (child != null) {
          child.parentNode = grand;
      }
    
      // 更新 grand 的 parent
      grand.parentNode = parent;
    
      // 更新高度
      updateHeight(grand);
      updateHeight(parent);
  }

4.2.5. 删除节点 - afterRemove()

• 我们基于 BST 进行开发，当我们新添加元素时需要保证 AVL 和 BST 互不影响。

  • 我们需要在 BST.java 中修改 remove() ，如果是基于 AVL 那么则需要进行删除节点之后进行处理。

  /**
   * 删除元素
   *
   * @param node 节点
   */
  private void remove(Node<E> node) {
      if (node == null) {
          return;
      }
    
      // 如果 node 是为删除度为1的节点
      if (removeNode != null) {
          // TODO ...
          
          // 删除之后的处理
          afterRemove(node);
      } else if (node.parentNode == null) { // 删除叶子节点, 且只有根节点元素
          root = null;
          // 删除之后的处理
          afterRemove(node);
      } else { // 删除叶子节点, 有可能当前节点在父级节点的左边，也有可能在父级节点的右边
          // TODO ...
          // 删除之后的处理
          afterRemove(node);
      }
      size--;
  }

  • 由于 AVL.java 继承了 BST.java 所以在 BST 中需要重写 afterRemove()

  /**
   * 删除之后做处理
   *
   * @param node 节点信息
   */
  @Override
  protected void afterRemove(Node<E> node) {
      while ((node = node.parentNode) != null) {
          // 判断整棵树是否平衡，如果平衡，则更新高度，如果不平衡，则恢复平衡
          if (isBalanced(node)) {
              // 更新高度
              updateHeight(node);
          } else {
              // 恢复平衡
              rebalanced(node);
          }
      }
  }

4.3. 总结

• 添加
  • 可能会导致所有的祖先节点都失衡
  • 只要让高度最低的失衡节点恢复平衡，整棵树就会恢复平衡【仅需O(1)次调整】
• 删除
  • 可能会导致父节点或祖先节点失衡
  • 恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要O(logn)次调整】
• 平均时间复杂度
  • 搜素：O(logn)
  • 添加：O(logn)，仅需O(1)次旋转
  • 删除：O(logn)，最多需要O(logn)次旋转操作

4.4. 单元测试

public class AVLTest {

    private AVL<Integer> avlTree;

    @BeforeEach
    void setUp() {
        avlTree = new AVL<>();
        // 添加一些元素作为测试数据
        avlTree.add(5);
        avlTree.add(3);
        avlTree.add(7);
        avlTree.add(2);
        avlTree.add(4);
        avlTree.add(6);
        avlTree.add(8);
    }

    @Test
    void testSizeAndClear() {
        assertEquals(7, avlTree.size());
        assertFalse(avlTree.isEmpty());

        avlTree.clear();

        assertEquals(0, avlTree.size());
        assertTrue(avlTree.isEmpty());
    }

    @Test
    void testBalanceAfterAdd() {
        // 添加节点后，检查 AVL 树是否保持平衡
        assertTrue(isBalanced(avlTree.root));
    }

    @Test
    void testBalanceAfterRemove() {
        // 在移除节点后，检查 AVL 树是否保持平衡
        avlTree.remove(3);
        assertTrue(isBalanced(avlTree.root));
    }

    private boolean isBalanced(BinaryTree.Node<Integer> node) {
        if (node == null) {
            return true;
        }
        int balanceFactor = ((AVL.AVLNode<Integer>) node).balanceFactor();
        return Math.abs(balanceFactor) <= 1 && isBalanced(node.leftNode) && isBalanced(node.rightNode);
    }
}

---

5. 参考博文

• 恋上数据结构与算法(第一季)-MJ大神精选