数据结构-红黑树

1. 内容大纲

本章节需要用到前面章节：二叉树、平衡二叉树、B树的知识。

本章节代码：https://github.com/wicksonZhang/data-structure/tree/main/8-RedBlackTree

---

2. 基础知识

2.1. 什么是红黑树

红黑树是在 AVL 树和 B 树基础上面进行发展而来的，所以红黑树也是一种自平衡的二叉搜索树。

2.2. 红黑树优缺点

优点

1. 平衡性：红黑树是基于二叉查找树（BST）的一种改进和扩展，这也确保了树的高度不会过高。
2. 高效的插入和删除：红黑树主要还是基于 AVL 和 B 两种数据结构进行历史演进而来，红黑树解决了 AVL 频繁插入、删除的问题。所以使得插入、删除和搜索等操作的时间复杂度可以保持在对数级别（O(log n)）。

缺点

1. 复杂性：红黑树结合了 B 树和 AVL 树的特性，导致添加和删除时需要涉及到元素的左旋和右旋，这也使得了红黑树的实现和理解稍微复杂一些。

2.3. 红黑树解决了什么问题

1. 红黑树主要解决了二叉查找树可能出现的不平衡性问题。

   • 二叉查找树的不平衡可能会导致性能退化，使得搜索、插入和删除等操作的时间复杂度从理想的 O(log n) 变为最坏情况下的 O(n)

2. AVL 树也解决了二叉搜索树可能出现的不平衡问题， 红黑树相比于 AVL 树又做了哪些优化呢？

   • 平衡调整的频率

     • AVL 树在频繁的插入和删除时会导致整棵树进行频繁的调整，这也需要更多的旋转操作，这会导致整棵树的性能下降。
     • 红黑树 红黑树采用通过颜色标记和一系列的平衡规则来确保整棵树的平衡，尤其是涉及到大量的插入和删除操作时尤为明显。

2.4. 生活中对应的场景

1. java 中的 HashMap 、TreeMap 集合就采用到了红黑树。

---

3. 红黑树的基本特性（重要）

3.1. 红黑树的性质

红黑树必须满足以下 5 条性质

1. 节点是 Red 或者 Black
2. 根节点是 Black
3. 叶子节点（外部节点、空节点） 都是 Black
4. Red 节点的子节点都是 Black
   1. Red 节点的 parent 都是 Black
   2. 根节点到叶子节点的所有路径上不能又 2 个连续的 Red 节点
5. 从任意节点到 叶子节点 的所有路径都包含相同数据的 Black 节点

3.2. 红黑树的等价交换

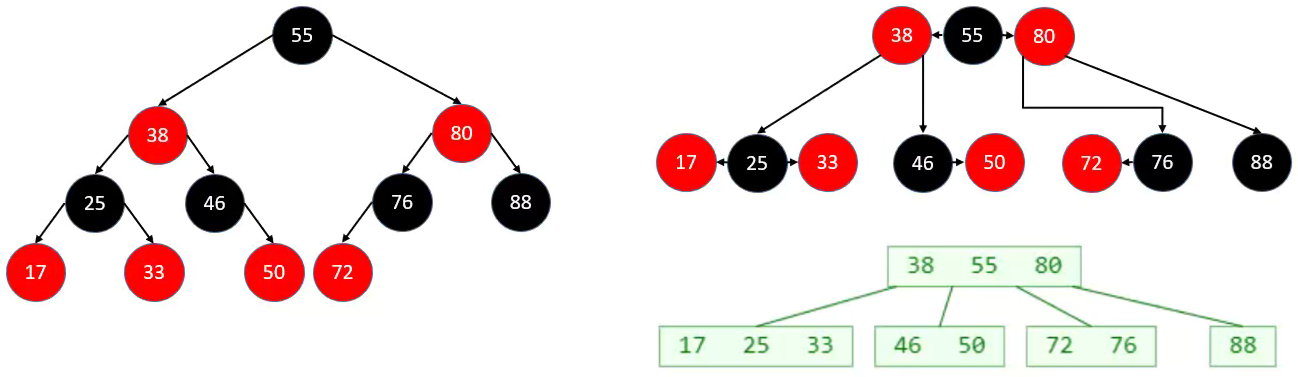
红黑树 和 4阶B树（2-3-4 树）具有等价性。

Black 和 Red 子节点融合在一起可以形成一个B树节点。

红黑树的 Black 节点个数与 4阶B树 的节点总个数相等。

---

4. 红黑树的实现

https://github.com/wicksonZhang/data-structure/tree/main/8-RedBlackTree

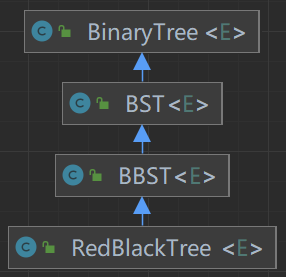
4.1. UML 类图

4.2. 红黑树添加元素

在 B 树中，新添加的元素必定会被添加到叶子节点中。

4阶B树中所有节点的元素个数 x 都满足 1 <= x <= 3。

我们基于如下图的红黑树，如果新增一个新元素有多少种情况？

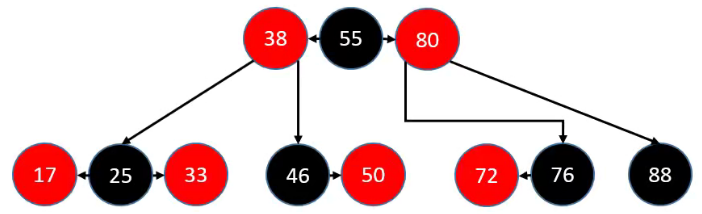
一共会有 12 种情况，假设所有添加的情况为x，具体如下：

1. 节点 17 的左右子节点，即两种情况，x = 2
2. 节点 33 的左右子节点，即两种情况, x = 4
3. 节点 46 的左子节点，即1种情况，x = 5
4. 节点 50 的左右子节点，即两种情况，x = 7
5. 节点 72 的左右子节点，即两种情况，x = 9
6. 节点 76 的右子节点，即两种情况，x = 10
7. 节点 88 的左右子节点，即两种情况，x = 12

4.3. 红黑树添加元素存在的问题

1. 添加新元素中存在什么问题？

   • 虽然我们添加新元素会存在 12 种情况，但是在 红黑树的5条基本特性 中的第四条有如下几条规定，增加了添加的不确定性：

   • 第一条：Red 节点的子节点都是 Black

   • 第二条：Red 节点的 parent 都是 Black

   • 第三条：根节点到叶子节点的所有路径上不能又 2 个连续的 Red 节点

2. 针对 Red 节点的子节点都是 Black 这种情况，有如下四种添加情况以满足，所以不用进行处理：

   • 节点 46 的左子节点

   • 节点 76 的右子节点

   • 节点 88 的左右子节点

   

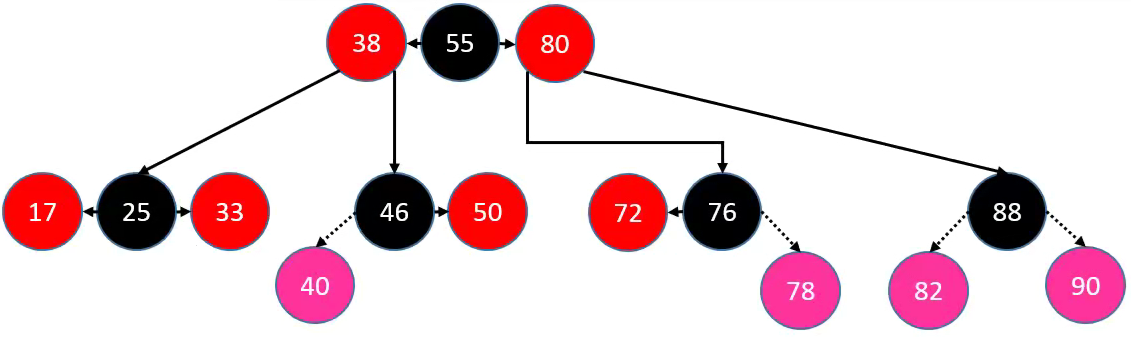
3. 针对 Red 节点的 parent 都是 Black 这种情况，有如下八种添加情况不满足：

   • 节点 17 的左右子节点
   • 节点 33 的左右子节点
   • 节点 50 的左右子节点
   • 节点 72 的左右子节点

   

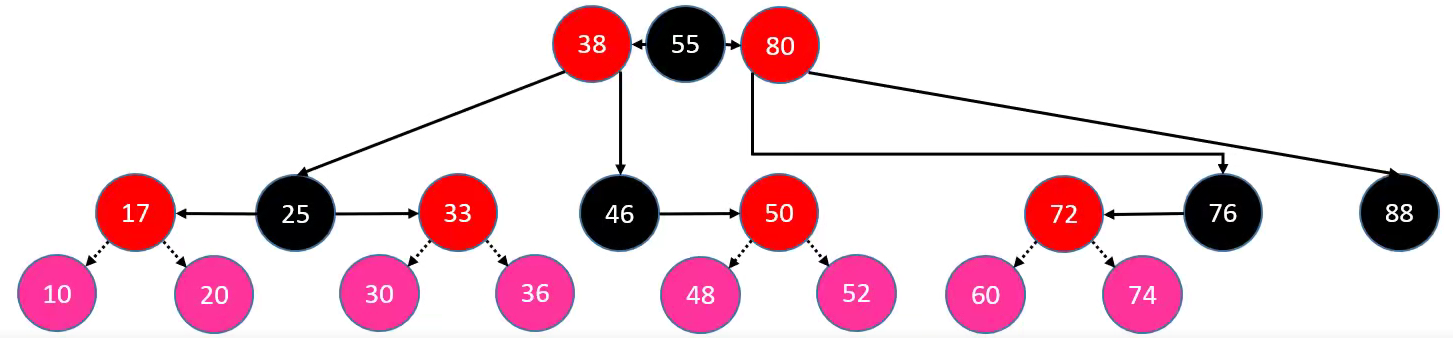
4.4. 修复红黑树添加存在的问题

针对上面八种添加存在的问题，我们分为两种情况处理：

• 情况一：uncle 节点是 Black 。
• 情况二：uncle 节点是 Red。

4.4.1. uncle 节点是 Black

添加节点 uncle 节点是 Black 的有节点 50 的左右子节点（48，52）、节点 72 的左右子节点（60，74），针对这四个节点我们采取如下方式处理：

1. 符合 LL 情况的节点：60
2. 符合 RR 情况的节点：52
3. 符合 LR 情况的节点：74
4. 符合 RL 情况的节点：48

4.4.1.1. 符合 LL 情况

符合 LL 情况的节点是 60 ，我们在 AVL 章节中给出的方式是进行右旋转即可。

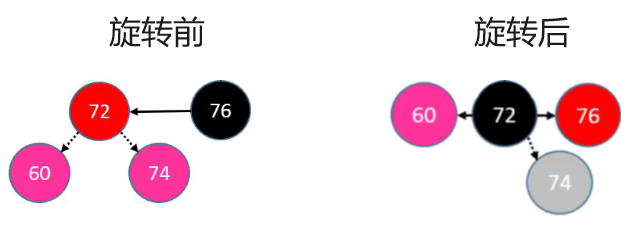
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。
2. 然后，将 grand 节点染成红色。
3. 最后，将 grand 节点进行右旋。

4.4.1.2. 符合 RR 情况

符合 RR 情况的节点是 52 ，我们在 AVL 章节中给出的方式是进行左旋转即可。

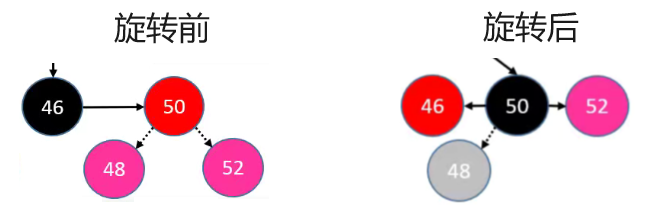
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。
2. 然后，将 grand 节点染成红色。
3. 最后，将 grand 节点进行左旋。

4.4.1.3. 符合 LR 情况

符合 LR 情况的节点是 74，我们在 AVL 章节中给出的方式是先进行左旋转，在进行右旋转。

具体的实现步骤如下：

1. 首先，将 grand 节点染成红色。

2. 然后，将 node 节点染成黑色。

3. 其次，将 parent 进行左旋转，将二叉树变为 LL（76 -> 74 -> 72 -> 60）
4. 最后，将 grand 进行一次右旋转，使二叉树变得平衡（76 <- 74 -> 72 -> 60）

4.4.1.4. 符合 RL 情况

符合 RL 情况的节点是 48，我们在 AVL 章节中给出的方式是先进行右旋转，在进行左旋转。

具体的实现步骤如下：

1. 首先，将 grand 节点染成红色。

2. 然后，将 node 节点染成黑色。

3. 其次，将 parent 进行右旋转，将二叉树变为 RR（46 -> 48 -> 50 -> 52）
4. 最后，将 grand 进行左旋转，使二叉树变得平衡（46 <- 48 -> 50 -> 52）

4.4.2. uncle 节点是 Red

添加节点 uncle 节点是 Red 的有节点 17 的左右子节点（10，20）、节点 33 的左右子节点（30，36），针对这四个节点我们采取如下方式处理：

• 符合上溢 LL 情况的节点：10
• 符合上溢 RR 情况的节点：36
• 符合上溢 LR 情况的节点：20
• 符合上溢 RL 情况的节点：30

4.4.2.1. 符合上溢 LL 情况

符合 LL 情况的节点是 10。这里需要使用到 B 树的特性，由于该树是 3 阶B树，3阶B树的根节点的子节点的个数为 [ 2, 3 ]，如果超过了就需要进行上溢。

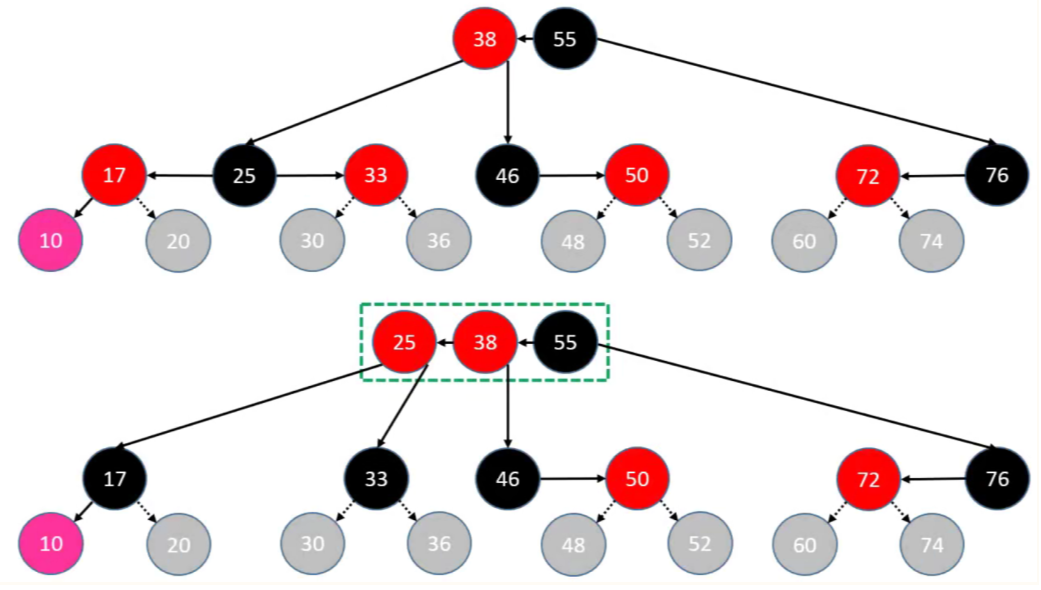
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。
2. 然后，将 uncle 节点染成黑色。
3. 其次，将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。
4. 最后，如果向上合并时，还出现上溢，则持续进行上溢到根节点，将根节点染成 Black。

4.4.2.2. 符合上溢 RR 情况

符合 RR 情况的节点是 36。这里需要使用到 B 树的特性，由于该树是 3 阶B树，3阶B树的根节点的子节点的个数为 [ 2, 3 ]，如果超过了就需要进行上溢。

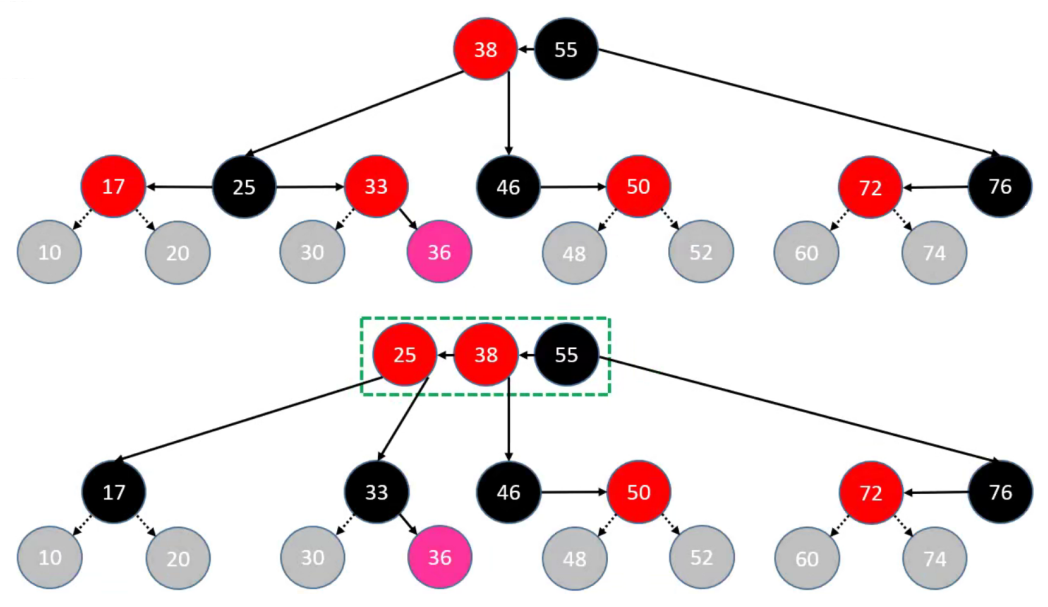
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。

2. 然后，将 uncle 节点染成黑色。

3. 其次，将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。

4. 最后，如果向上合并时，还出现上溢，则持续进行上溢到根节点，将根节点染成 Black。

4.4.2.3. 符合上溢 LR 情况

符合上溢 LR 情况的节点是 20。这里需要使用到 B 树的特性，由于该树是 3 阶B树，3阶B树的根节点的子节点的个数为 [ 2, 3 ]，如果超过了就需要进行上溢。

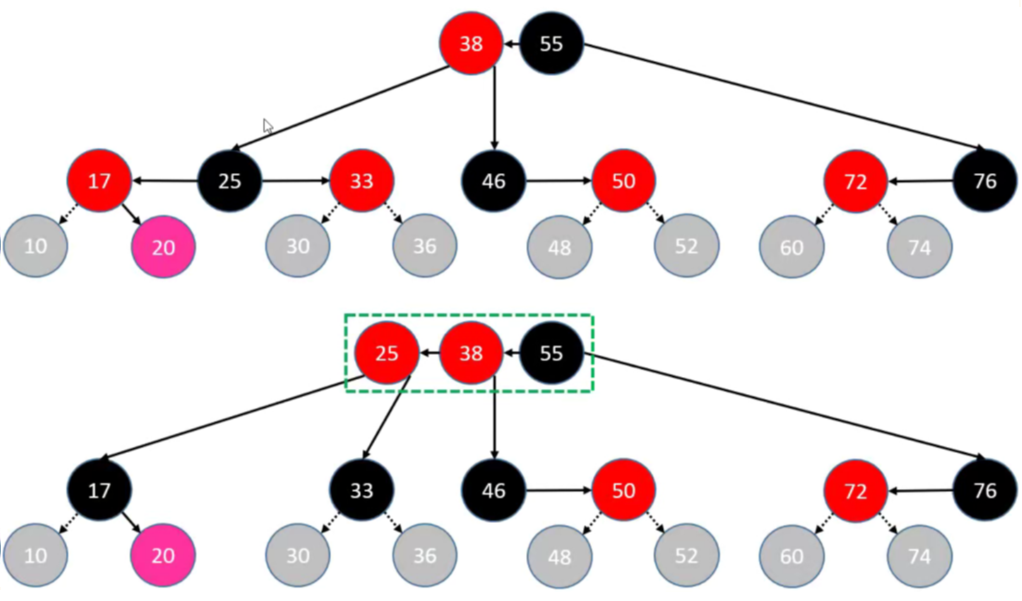
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。

2. 然后，将 uncle 节点染成黑色。

3. 其次，将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。

4. 最后，如果向上合并时，还出现上溢，则持续进行上溢到根节点，将根节点染成 Black。

4.4.2.4. 符合上溢 RL 情况

符合上溢 RL 情况的节点是 30。这里需要使用到 B 树的特性，由于该树是 3 阶B树，3阶B树的根节点的子节点的个数为 [ 2, 3 ]，如果超过了就需要进行上溢。

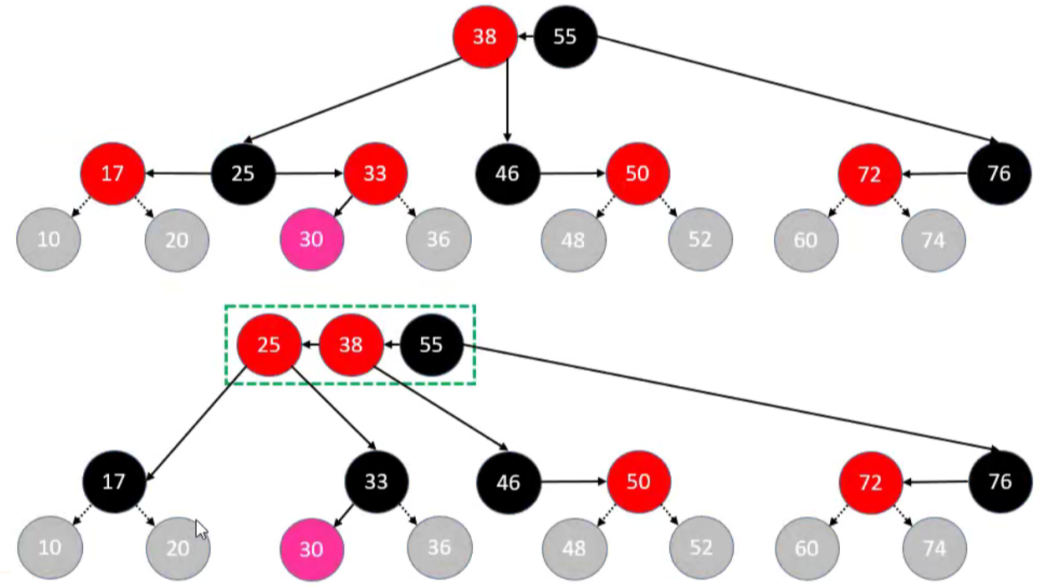
具体的实现步骤如下：

1. 首先，将 parent 节点染成黑色。

2. 然后，将 uncle 节点染成黑色。

3. 其次，将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。

4. 最后，如果向上合并时，还出现上溢，则持续进行上溢到根节点，将根节点染成 Black。

4.5. 红黑树删除元素

我们删除需要明确的一点是：在删除中，最后真正被删除的一定是叶子节点

我们上面说过，最后一定删除的是叶子节点。那么上图中就会存在两种情况，叶子节点为红色或者黑色。

1. 叶子节点为红色

   • 叶子节点为红色的情况不需要进行处理。例如，不管是删除17、33、50、72 都是一样，不会改变红黑树的性质。

   

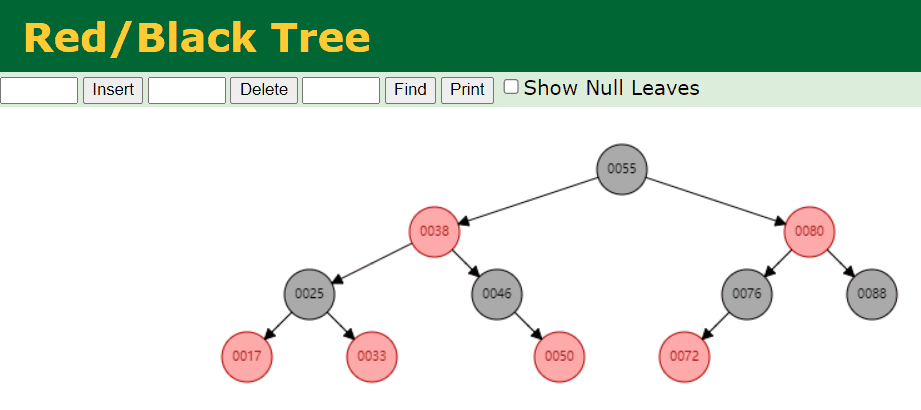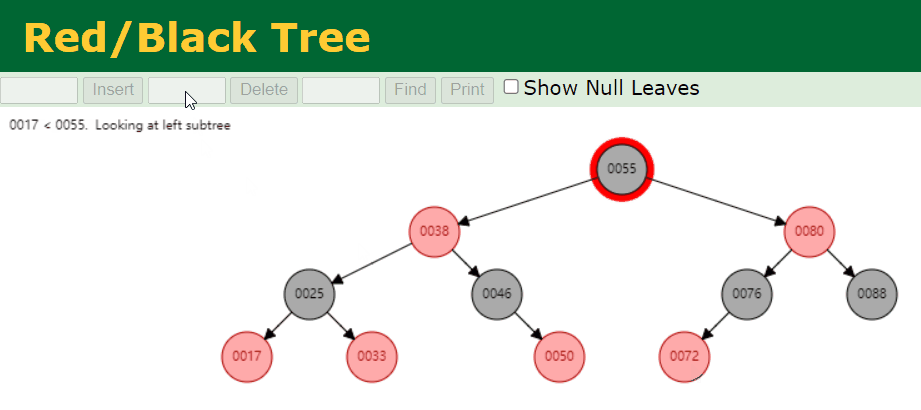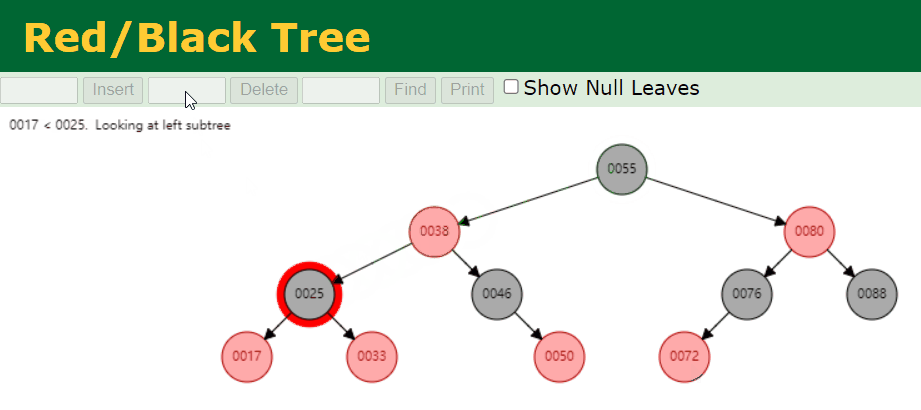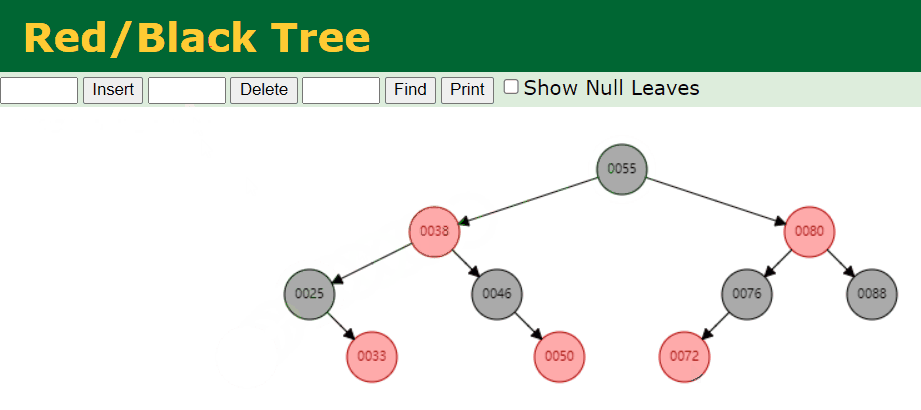
2. 叶子节点为黑色

   • 我们删除拥有 2 个 Red 子节点的 Black 节点。例如，我们删除的是 25 这个节点，具体情况如下：

   

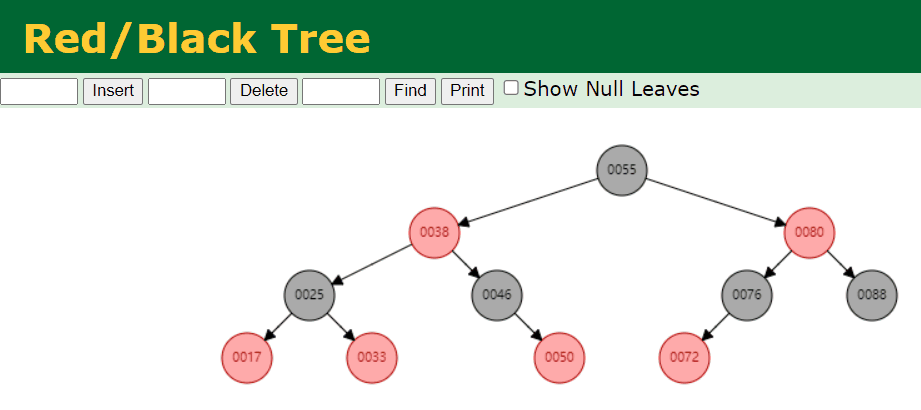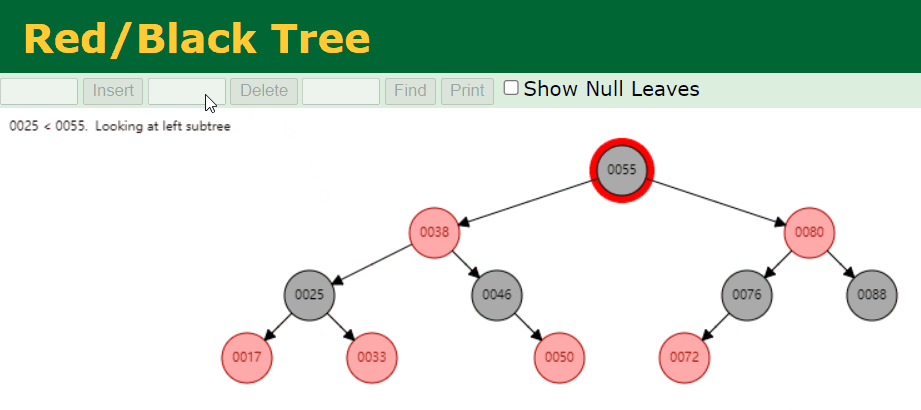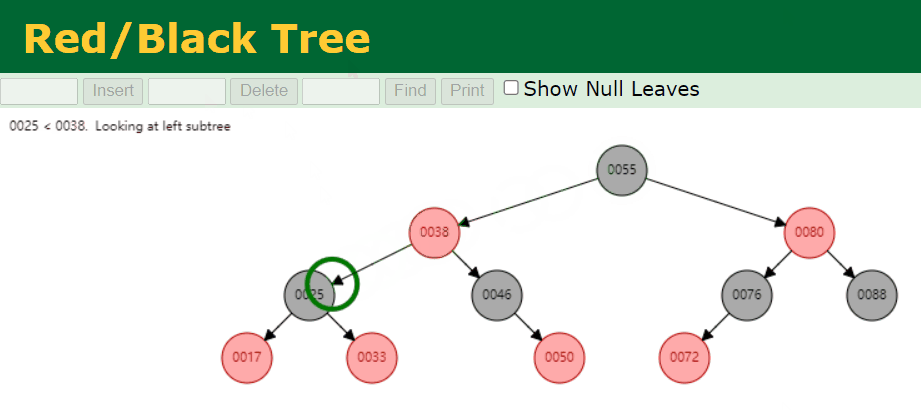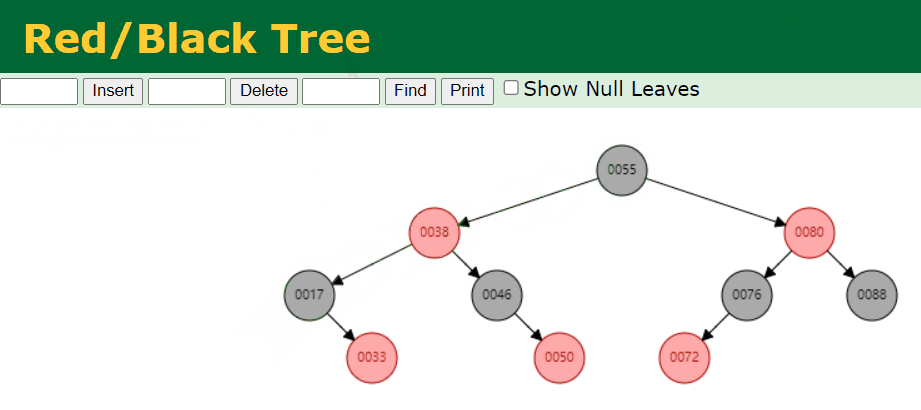
   • 我们删除拥有 1 个 Red 子节点的 Black 节点。例如，我们删除的是 46 这个节点，具体情况如下：

   

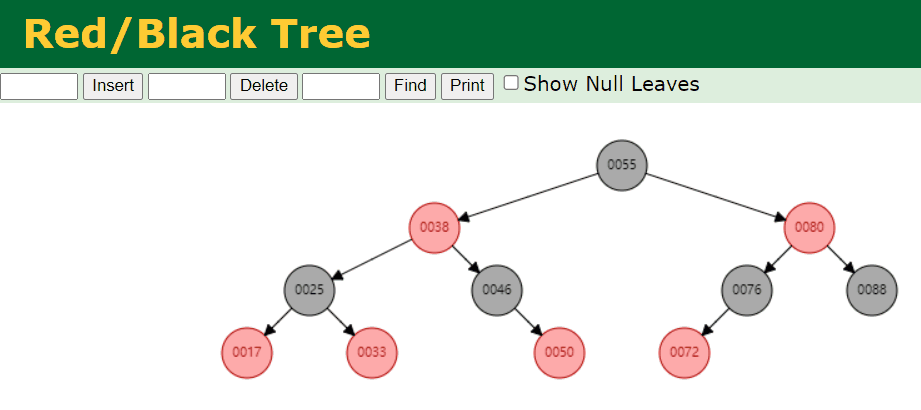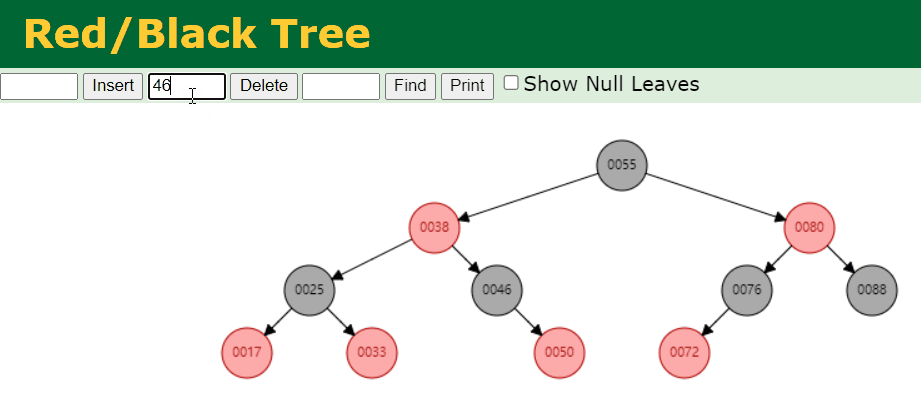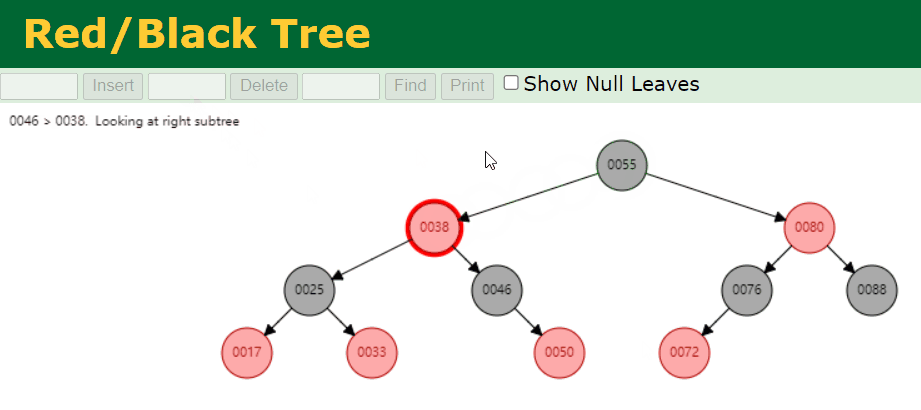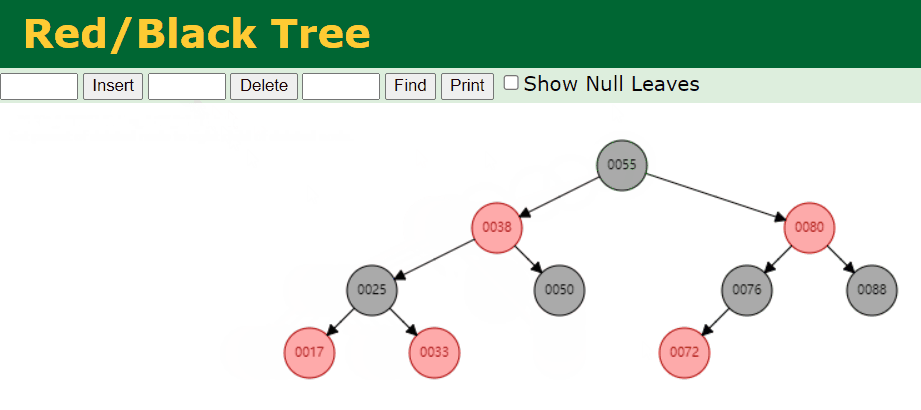
   • 我们删除叶子节点 Black 节点。例如，我们删除的是 88 这个节点，具体情况如下：

   

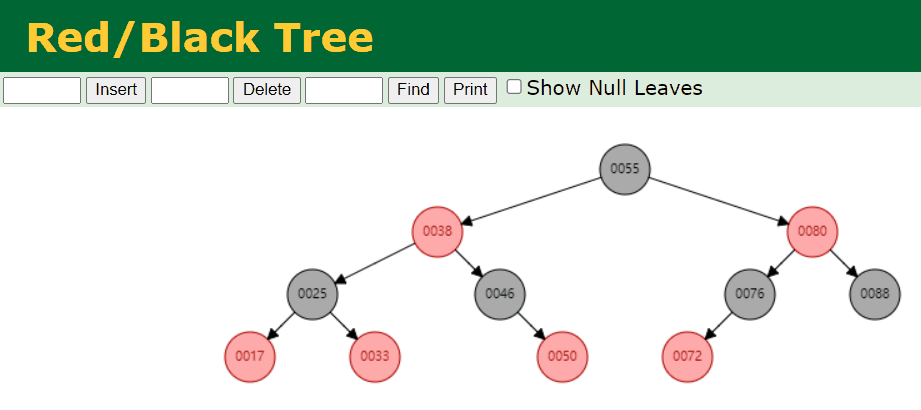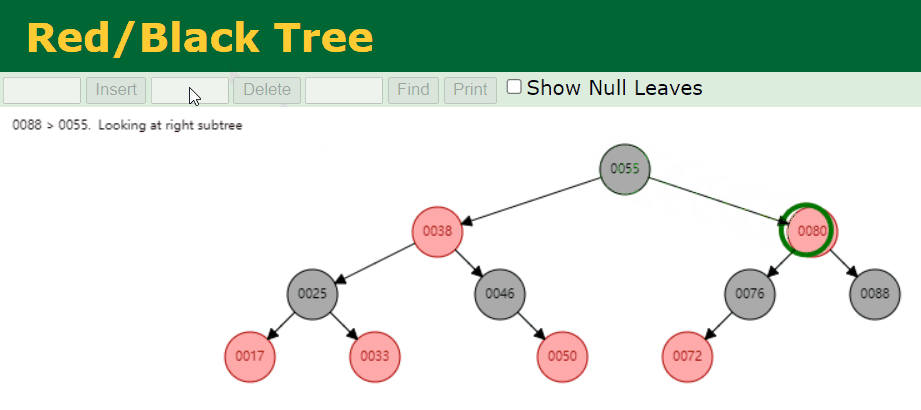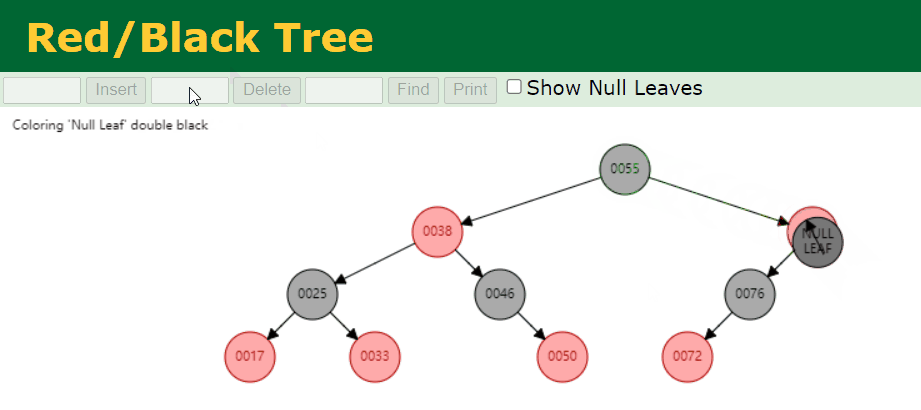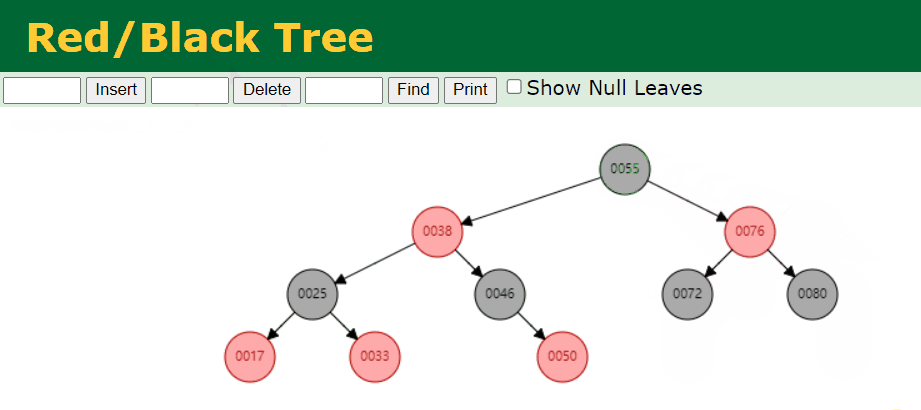
4.6. 修复删除存在的问题

4.6.1. 删除叶子节点为红色

如果叶子节点为红色，我们是不用进行任何处理的。因为并不会影响我们红黑树的特性

4.6.2. 删除叶子节点为黑色

我们将上面示例的图转变为 B 树进行处理，具体如下：

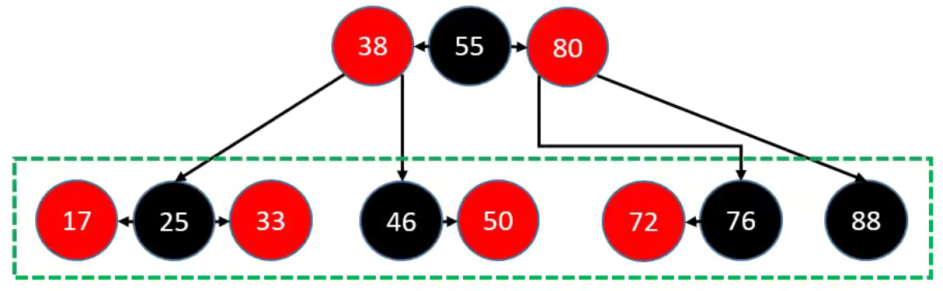
4.6.2.1. 2 个 Red 子节点的 Black

符合 2 个 Red 子节点的 Black 节点 的节点是 25，我们这对这个情况进行处理。

实现思路：

1. Step-1：首先，我们找到被删除节点的前驱节点 17 。
2. Step-2：然后，我们将前驱节点 17 覆盖掉节点 25 的值。
3. Step-3：其次，删除节点 17。
4. Step-4：我们将节点 17 传入给红黑树，但前面已经说过了叶子节点为红色不用处理。

4.6.2.2. 1 个 Red 子节点的 Black

符合 1 个 Red 子节点的 Black 节点 的节点是 46，我么针对这个情况进行处理。

实现思路：

1. Step-1：首先，找到被删除节点 46 的前驱或者后继节点。
2. Step-2：然后，更换父级节点。将节点 46 的父级节点指向节点 50。
3. Step-3：其次，更换节点位置。将节点 46 的父级节点的右子节点指向节点 50。
4. Step-4：最后，我们将节点 50 染成黑色。

4.6.2.3. 叶子节点 Black

情况一：删除的 Black 的叶子节点 sibling 为 Black，且至少存在红色子节点

• 符合 叶子节点 Black 节点 的节点是 88，我么针对这个情况进行处理。

  

实现思路

1. Step-1：当叶子节点 Black 被删除时，会导致 B 树进行下溢。
2. Step-2：如果 sibling 至少有 1 个 Red 子节点，我们则进行旋转操作。
3. Step-3：旋转之后的中心节点继承 parent 的颜色。
4. Step-4：旋转之后的左右节点染成 Black。

情况二：删除的 Black 的叶子节点 sibling 为 Black，且不存在红色子节点

• 符合 叶子节点 Black 节点 的节点是 88，我么针对这个情况进行处理。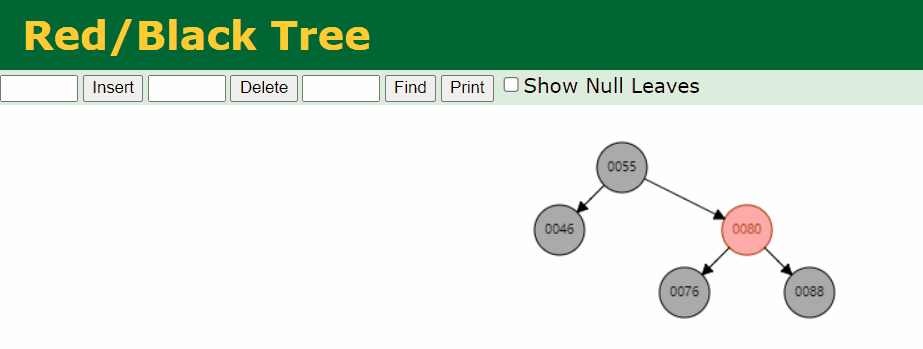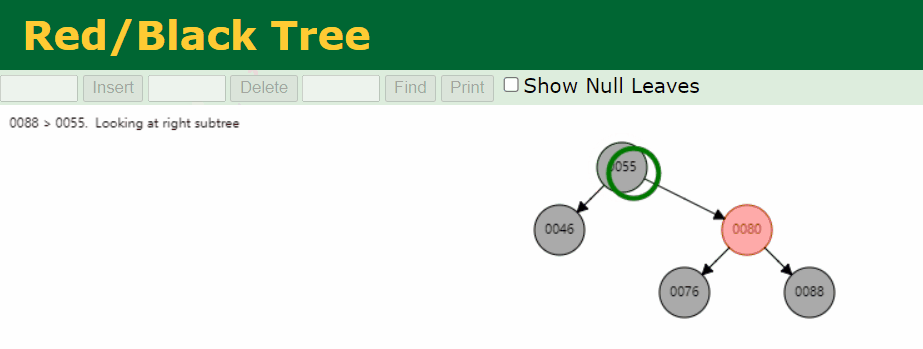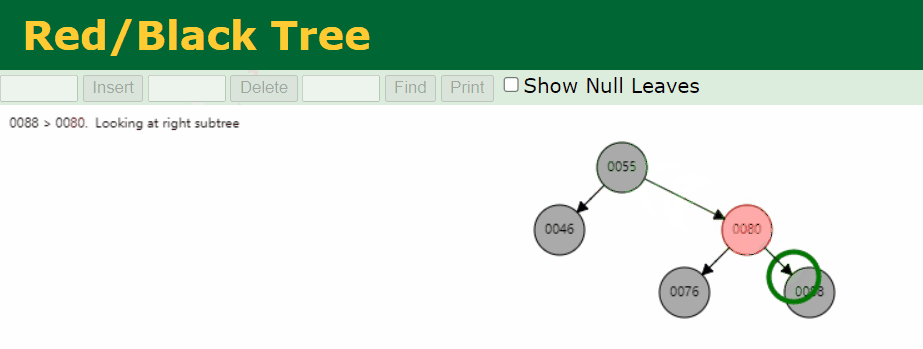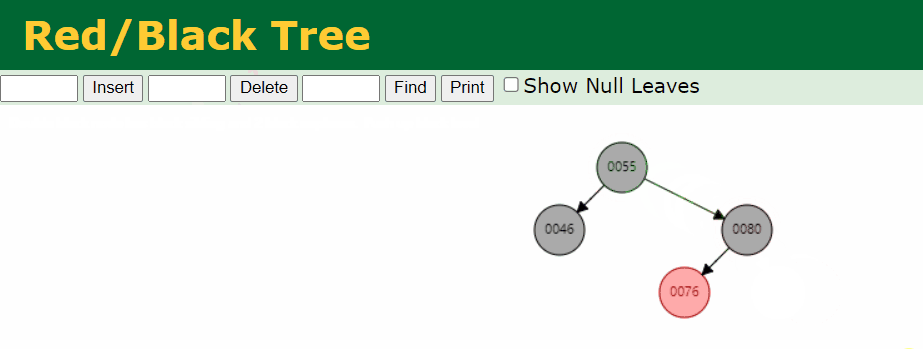

  

实现思路

1. Step-1：判定条件，sibling没有 1 个 Red 子节点
2. Step-2：将 sibling 染成 Red、parent 染成 Black 即可修复红黑树性质

情况三：删除的 Black 的叶子节点 sibling 为 Red

• 符合 叶子节点 Black 节点 的节点是 88，我么针对这个情况进行处理。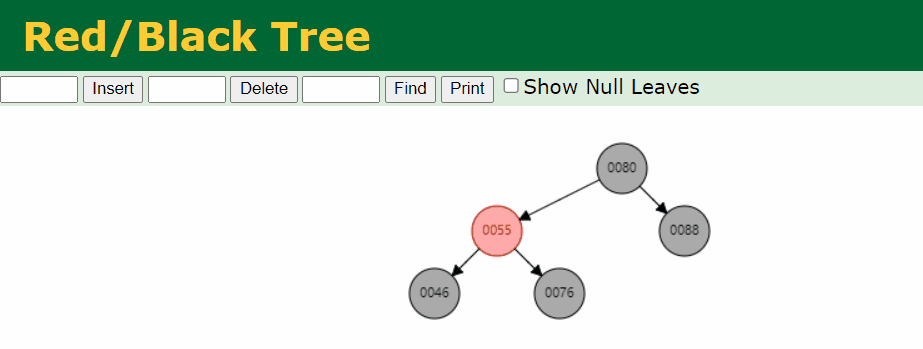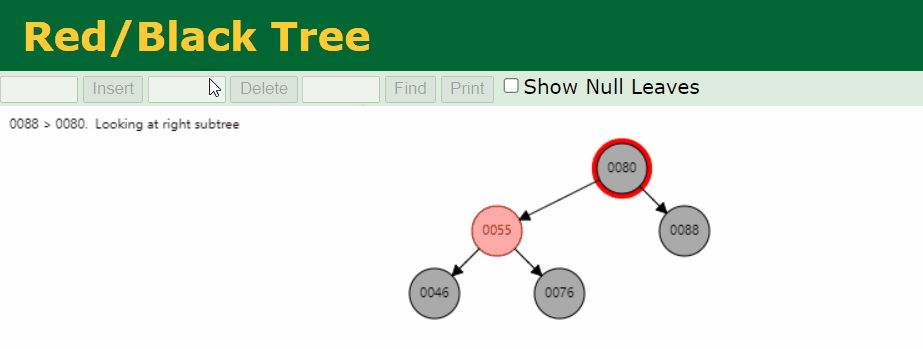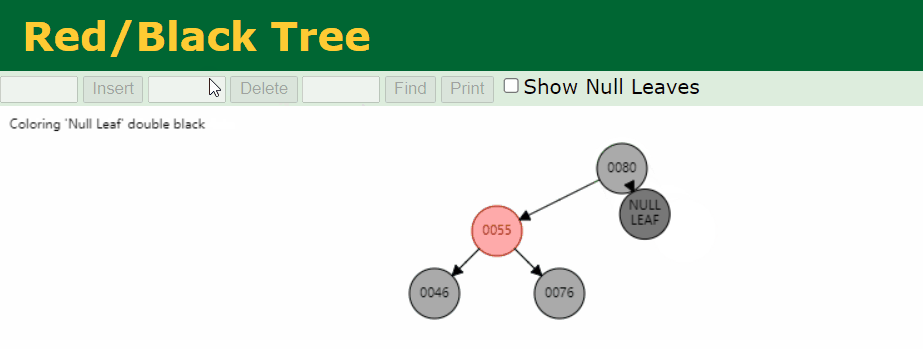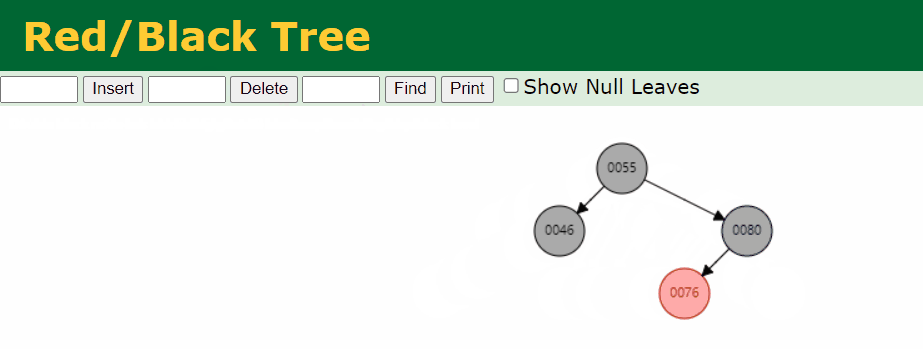

  

实现思路

1. Step-1：将 sibling 染成 Black，parent 染成 Red，进行旋转

2. Step-2：于是又回到了 sibling 为 Black 的情况

4.7. 代码实现

4.7.1. 构造器

上面已经说过了红黑树是来源于 AVL 树和 B 树，所以我们的代码还是基于二叉树进行开发。

/**
 * 红黑树
 */
public class RedBlackTree<E> extends BST<E> {

    public RedBlackTree() {
        this(null);
    }

    public RedBlackTree(Comparator<E> comparator) {
        super(comparator);
    }
    
    // 红色节点
    private static final boolean RED = false;

    // 黑色节点
    private static final boolean BLACK = true;
    
    /**
     * 创建红黑树节点
     *
     * @param element 元素信息
     * @param parent  父级节点信息
     * @return Node<E>
     */
    @Override
    protected Node<E> createNode(E element, Node<E> parent) {
        return new RedBlackNode<>(element, parent);
    }

    /**
     * 红黑树节点
     *
     * @param <E>
     */
    private static class RedBlackNode<E> extends Node<E> {
        boolean color = RED;

        public RedBlackNode(E element, Node<E> parentNode) {
            super(element, parentNode);
        }
    }

}

4.7.2. 红黑树的辅助节点

基于上面的构造器的信息，但是我们针对红黑树也有一些定制化的开发。

红黑树的辅助节点代码

• 对添加的节点进行染色
• 添加红色或者黑色节点
• 判断红黑树节点的颜色
• 返回当前节点的兄弟节点

4.7.2.1. 对添加的节点进行染色

• 我们对添加的节点进行染色时，需要将 BST 的节点强制转换红黑树的节点进行染色。

/**
 * 对添加节点进行染色
 *
 * @param node  节点
 * @param color 颜色
 * @return Node<E>
 */
private Node<E> color(Node<E> node, boolean color) {
    if (node == null) return null;

    ((RedBlackNode<E>) node).color = color;
    return node;
}

4.7.2.2. 添加红色或者黑色节点

• 我们基于 对添加的节点进行染色 代码进行扩展，可以添加红色节点或者添加黑色节点。

/**
 * 添加红色节点
 *
 * @param node 节点
 * @return Node<E>
 */
private Node<E> red(Node<E> node) {
    return color(node, RED);
}

/**
 * 添加黑色节点
 *
 * @param node 节点
 * @return Node<E>
 */
private Node<E> black(Node<E> node) {
    return color(node, BLACK);
}

4.7.2.3. 判断红黑树节点的颜色

/**
 * 判断红黑树节点的颜色
 *
 * @param node 节点
 * @return boolean
 */
private boolean colorOf(Node<E> node) {
    return node == null ? BLACK : ((RedBlackNode<E>) node).color;
}

/**
 * 判断是否是红色节点
 *
 * @param node 节点
 * @return boolean
 */
private boolean isRed(Node<E> node) {
    return colorOf(node) == RED;
}

/**
 * 判断是否是红色节点
 *
 * @param node 节点
 * @return boolean
 */
private boolean isBlack(Node<E> node) {
    return colorOf(node) == BLACK;
}

4.7.2.4. 返回当前节点的兄弟节点

• 该方法是在 BinaryTree 中 Node<E> 进行添加

/**
 * 兄弟节点
 *
 * @return Node<E>
 */
public Node<E> sibling() {
    if (isLeftChild()) {
        return parentNode.rightNode;
    }
    if (isRightChild()) {
        return parentNode.leftNode;
    }
    return null;
}

4.7.3. 添加

我们只需要按照 修复添加存在的问题 中的思路进行实现即可

• 添加代码如下

/**
 * @param node 节点信息
 */
@Override
protected void afterAdd(Node<E> node) {
    // 判断当前添加的父级节点
    Node<E> parentNode = node.parentNode;
    if (parentNode == null) {
        black(node);
        return;
    }

    /* Step-1：添加的节点父节点正好是 black */
    if (isBlack(parentNode)) {
        return;
    }

    /* Step-2：添加的节点 `uncle` 节点是 `Red` */
    // 叔父节点
    Node<E> uncle = parentNode.sibling();
    // 祖父节点
    Node<E> grandNode = parentNode.parentNode;
    if (isRed(uncle)) {
        // 将 parent 节点染成黑色
        black(parentNode);
        // 将 uncle 节点染成黑色
        black(uncle);
        // 将 grand 节点染成红色，向上进行合并，当作新添加的节点进行处理。
        afterAdd(red(grandNode));
        return;
    }

    /* Step-3：添加的节点 `uncle` 节点是 `Black` */
    // 判断父级节点是否是左子节点
    if (parentNode.isLeftChild()) { // L
        // 将 `grand` 节点染成红色
        red(grandNode);
        // 判断自己是否是左子节点
        if (node.isLeftChild()) { // LL
            // 将 `parent` 节点染成黑色
            black(parentNode);
        } else { // LR
            // 将 `parent` 节点染成黑色
            black(node);
            // 将 `parent` 进行左旋转，将二叉树变为 `LL`
            rotateLeft(parentNode);
        }
        // 将 `grand` 节点进行右旋
        rotateRight(grandNode);
    } else { // R
        // 将 `grand` 节点染成红色
        red(grandNode);
        if (node.isRightChild()) { // RR
            // 将 `parent` 节点染成黑色
            black(parentNode);
        } else { // RL
            // 将 `node` 节点染成黑色
            black(node);
            // 将 `parent` 进行右旋转，将二叉树变为 `RR`
            rotateRight(parentNode);
        }
        // 将 `grand` 进行左旋转，使二叉树变得平衡
        rotateLeft(grandNode);
    }
}

4.7.4. 删除

我们只需要按照 修复删除存在的问题 中的思路进行实现即可

• 添加代码如下

 	@Override
    protected void afterRemove(Node<E> node) {
        /* Step-1：如果叶子节点为红色，不用处理 */
//        if (isRed(node)) return;

        /* Step-2：1 个 Red 子节点的 Black 节点 */
        if (isRed(node)) {
            black(node);
            return;
        }

        // 删除的节点是根节点
        Node<E> parentNode = node.parentNode;
        if (parentNode == null) { return; }

        /* Step-3：叶子节点 Black 节点 */
        // leftNode == null =》 leftNode 就是被删除的节点
        boolean leftNode = parentNode.leftNode == null || node.isLeftChild();
        Node<E> siblingNode = leftNode ? parentNode.rightNode : parentNode.leftNode;
        if (leftNode) { // 被删除的节点在左边，兄弟节点在右边
            // 兄弟节点是红色
            if (isRed(siblingNode)) {
                black(siblingNode);
                red(parentNode);
                rotateLeft(parentNode);
                // 更换兄弟节点
                siblingNode = parentNode.rightNode;
            }
            // 兄弟节点必然是黑色
            if (isBlack(siblingNode.leftNode) && isRed(siblingNode.rightNode)) {
                // 兄弟节点没有 1 个红色子节点，父节点要向下跟兄弟节点合并
                boolean parentBlack = isBlack(parentNode);
                black(parentNode);
                red(siblingNode);
                if (parentBlack) {
                    afterRemove(parentNode);
                }
            } else {
                // 兄弟节点至少有 1 个红色子节点，向兄弟节点借元素
                if (isBlack(siblingNode.rightNode)) {
                    rotateRight(siblingNode);
                    siblingNode = parentNode.rightNode;
                }

                color(siblingNode, colorOf(parentNode));
                black(siblingNode.rightNode);
                black(parentNode);
                rotateLeft(parentNode);
            }
        } else { // 被删除的节点在右边，兄弟节点在左边
            // 兄弟节点是红色
            if (isRed(siblingNode)) {
                black(siblingNode);
                red(parentNode);
                rotateRight(parentNode);
                // 更换兄弟节点
                siblingNode = parentNode.leftNode;
            }
            // 兄弟节点必然是黑色
            if (isBlack(siblingNode.leftNode) && isRed(siblingNode.rightNode)) {
                // 兄弟节点没有 1 个红色子节点，父节点要向下跟兄弟节点合并
                boolean parentBlack = isBlack(parentNode);
                black(parentNode);
                red(siblingNode);
                if (parentBlack) {
                    afterRemove(parentNode);
                }
            } else {
                // 兄弟节点至少有 1 个红色子节点，向兄弟节点借元素
                if (isBlack(siblingNode.leftNode)) {
                    rotateLeft(siblingNode);
                    siblingNode = parentNode.leftNode;
                }

                color(siblingNode, colorOf(parentNode));
                black(siblingNode.leftNode);
                black(parentNode);
                rotateRight(parentNode);
            }
        }

    }

4.8. 单元测试

public class RedBlackTreeTest {

    @Test
    public void testAdd() {
        RedBlackTree<Integer> tree = new RedBlackTree<>();
        tree.add(10);
        tree.add(5);
        tree.add(15);
        assertEquals(3, tree.size());
        assertTrue(tree.contains(10));
        assertTrue(tree.contains(5));
        assertTrue(tree.contains(15));
    }

    @Test
    public void testRemove() {
        RedBlackTree<Integer> tree = new RedBlackTree<>();
        tree.add(10);
        tree.add(5);
        tree.add(15);
        tree.remove(5);
        assertEquals(2, tree.size());
        assertFalse(tree.contains(5));
    }

}

---

5. AVL树 、红黑树

1. AVL树
   • 平衡标准比较严格：每个左右子树的高度差不超过1
   • 最大高度是 1.44 * log2(n+ 2) - 1.328 （100 W个节点，AVL树最大树高28）
   • 搜索、添加、删除都是 O(logn) 复杂度,其中添加仅需 0(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整
2. 红黑树
   • 平衡标准比较宽松:没有一条路径会大于其他路径的2倍
   • 最大高度是 2 * log2(n+ 1) （100 W个节点,红黑树最大树高40）
   • 搜索、添加、删除都是 O(logn) 复杂度,其中添加、删除都仅需 0(1) 次旋转调整
3. 总结
   • 搜索、添加、删除都是 O(logn) 复杂度,其中添加、删除都仅需 0(1) 次旋转调整
   • 相对于 AVL 树来说，红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作，整体来说性能要优于 AVL 树
   • 红黑树的平均统计性能优于 AVL 树，实际应用中更多选择使用红黑树

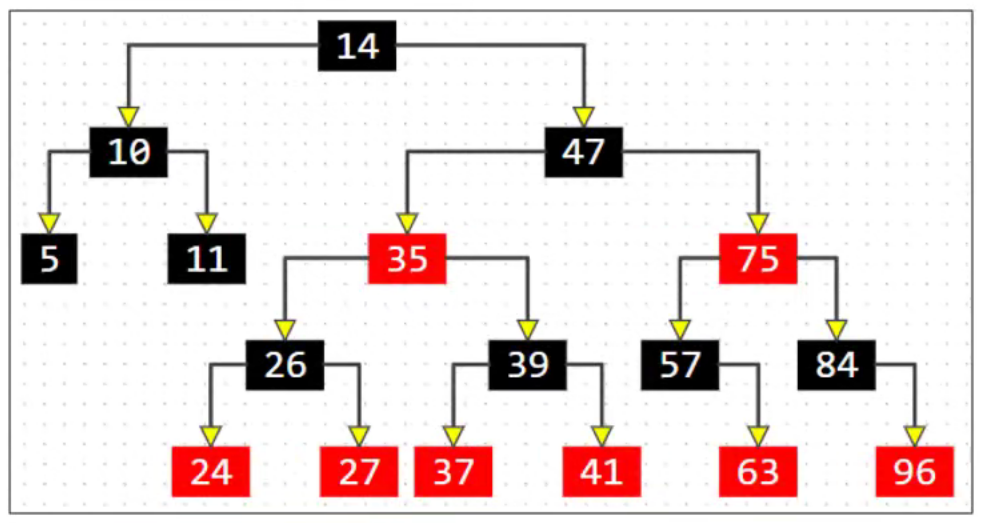
例如，我们插入数据 ：10、35、47、11、5、57、39、14、27、26、84、75、63、41、37、24、96 对比二叉搜索树、AVL树、红黑树的区别

二叉搜索树

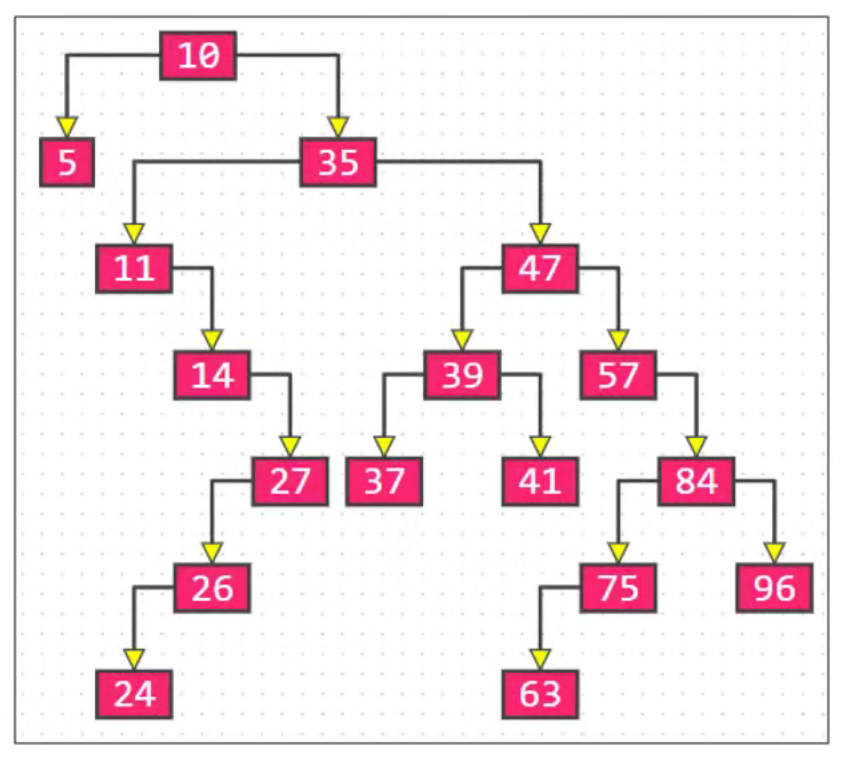
AVL 树

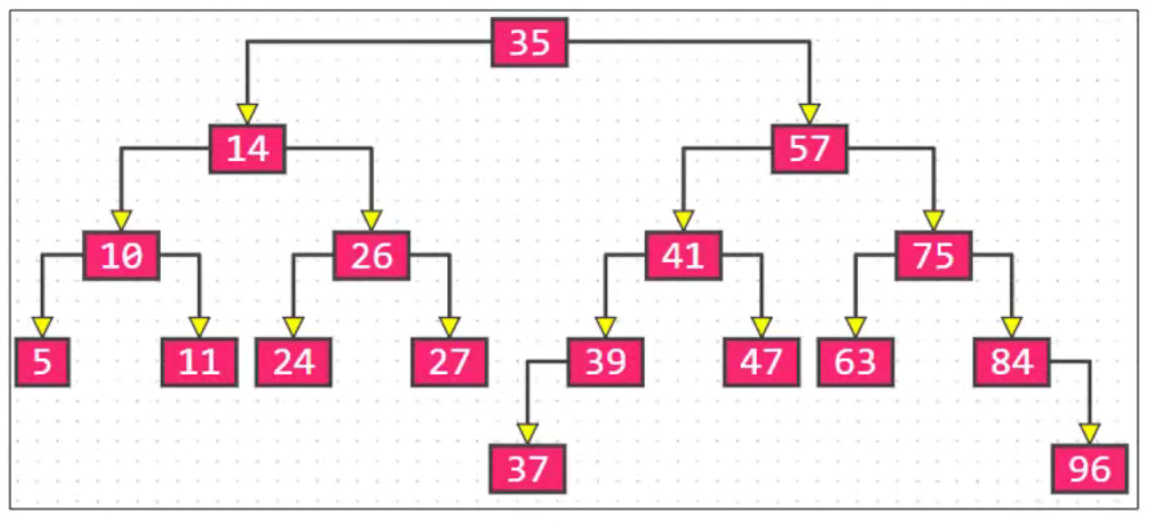
红黑树

---

6. 参考博文

• 恋上数据结构与算法(第一季)-MJ大神精选